Chapter 14: External Diffusion Effects on Heteregeneous Reactions

Topics

  1. Seven Steps in a Catalytic Reaction
  2. External Diffusion Across a Stagnant Film
  3. Relative Rates of Diffusion and Reaction
  4. Mass Transfer in a Packed Bed of Catalyst Particles
  5. Shrinking Core Model

The 7 Steps in a Catalytic Reaction

Top

1. Mass transfer (diffusion) of the reactant(s) from the bulk fluid to the external surface of the catalyst pellet

2. Diffusion of the reactant from the pore mouth through the catalyst pores to the immediate vicinity of the internal catalytic surface

3. Adsorption of reactant A onto the catalytic surface

4. Reaction on the surface of the catalyst

5. Desorption of the products from the surface

6. Diffusion of the products from the interior of the pellet to the pore mouth at the external surface

7. Mass transfer of the products from the external pellet surface to the bulk fluid

We shall now focus on steps 1, 2, 6, and 7. Because the reaction below does not occur in the bulk phase (only at the surface, at z = delta), we shall first consider steps 1 and 7.

Binary Diffusion

Diffusion is the spontaneous intermingling or mixing of atoms or molecules by random thermal motion. Mass transfer is any process in which diffusion plays a role.

The molar flux is just the molar flow rate, FA, divided by the cross sectional area, AC, normal to the flow. WA = FA/AC

Molar flux of A WA (moles/time/area) with respect to fixed coordinate system

WA = JA + BA

JA = diffusional flux of A with respect to bulk motion, i.e. molar average velocity

BA = flux of A resulting from bulk flow

\( W_A = J_A + y_A (W_A + W_B) \)

Derive Derive this equation

One dimension for constant total concentration- Ficks First Law

Biography Adolph Fick (1829-1901)

\( J_{Az} = -c D_{AB} \frac{dy}{dz} = -D_{AB} \frac{dC_A}{dz} \)

Constitutive Equation for Diffusion

\( W_{Az} = -D_{AB} \frac{dC_A}{dz} + y_A \left( W_{Az} + W_{Bz} \right) \)

\( W_{Az} = -D_{AB} \frac{dC_A}{dz} + C_A V_z \)

Gases: DAb~10-5m2/s

\( D_{AB}(T_2) = D_{AB}(T_1) \left( \frac{T_2}{T_1} \right)^{1.75} \left( \frac{P_1}{P_2} \right) \)

Liquids: DAb~10-9m2/s

\( D_{AB}(T_2) = D_{AB}(T_1) \left( \frac{T_2}{T_1} \right) \left( \frac{\mu_1}{\mu_2} \right) \)

Example Prediction of Gas Phase Diffusivities

External Diffusion Across a Stagnant Film

Top

Species A diffuses from the bulk (z=0) to a catalytic surface (z=d) where it reacts instantaneously to form B.

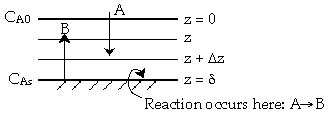
Diagram showing diffusion and reaction. Species A diffuses downward from concentration CA0 at z = 0 to CAS at z = δ. Species B diffuses upward. A reaction A → B occurs at the surface z = δ, indicated by a curved arrow and text 'Reaction occurs here: A → B'.

In-Out+Generation=Accumulation

\( W_A \big|_z - W_A \big|_{z + \Delta z} + 0 = 0 \)

\( \frac{dW_A}{dz} = 0 \)

\( W_A = -c D_{AB} \frac{dy_A}{dz} + y_A (W_A + W_B) \)

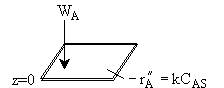
Types of Boundary Conditions

1. Specify a concentration a boundary

\( z = 0 \quad C_A = C_{A0} \)

\( z = \delta \quad C_A = C_{AS} \)

2. Specify a flux at a boundary

a) No mass transfer across a boundary

[E.g., at pipe wall]

\( W_{Ar} = 0 \quad \text{at} \quad r = R \)

therefore

\( \frac{dC_A}{dr} = 0 \quad \text{at} \quad r = R \)

b) Reaction at a boundary

\( W_A = -r'_A \quad \text{at} \quad z = 0 \quad (\text{surface}) \)

Diagram showing a surface at z = 0 with a downward arrow labeled W_A representing flux of species A. A reaction rate is noted on the surface as -rA'' = kCAS, indicating a first-order surface reaction dependent on the surface concentration CAS.

\( W_A - r''_A = k C_{AS} \)

c) Diffusional flux to a boundary is equal to the convective flux away from the boundary.

\( W_A(\text{boundary}) = k_c [C_{As} - C_{Ab}] \)

\(-D_{AB} \left. \frac{dC_A}{dZ} \right|_{z=0} = k_c [C_{As} - C_{Ab}] \)

Diagram showing mass transfer across a stagnant film of thickness δ, from z = δ to z = 0. At z = 0, the flux is expressed as kc[CAS − CAb], where kc is the mass transfer coefficient. At z = δ, the flux is given by −DAB dCA/dz, representing Fick's law. Concentrations CAS and CAb are labeled at their respective positions.

\( k_c [C_{As} - C_{Ab}] - D_{AB} \frac{dC_A}{dz} \)

3. Planes of Symmetry

[E.g., cylinder]

Circle representing a cross-section in cylindrical or spherical coordinates. The center is marked with a dot and labeled r = 0, indicating the origin.

\(\textbf{at } r = 0 \text{ then } \frac{dC_A}{dr} = 0\)

4 Common Cases of the Constitutive Equation

1) Dilute concentrations (liquids)

\( y_A (W_A + W_B) \approx 0 \)

Constant total concentration

\( W_{Az} = -D_{AB} \frac{dC_A}{dz} \)

\( W_{Az} = \frac{D_{AB}}{\delta} \left[ C_{A0} - C_{As} \right] \)

Derive Derive this equation

\( \frac{C_{A0} - C_A}{C_{A0} - C_{As}} = \frac{z}{\delta} \)

2) Equal Molar Counter Diffusion (EMCD)

\( W_A = -W_B \)

\( W_{Az} = -D_{AB} \frac{dC_A}{dz} \)

\( W_{Az} = \frac{D_{AB}}{\delta} \left[ C_{A0} - C_{As} \right] \)

\( \frac{C_{A0} - C_A}{C_{A0} - C_{As}} = \frac{z}{\delta} \)

3) Diffusion through a Stagnant Film

\( W_{Az} = K_1 \)

\( W_{Az} = -c D_{AB} \frac{dy_A}{dz} + y_A \left( W_{Az} + W_{Bz} \right) \)

\( W_{Az} = \frac{c D_{AB}}{\delta} \ln \left( \frac{1 - y_{As}}{1 - y_{A0}} \right) \)

Derive Derive this equation

\( \frac{1 - y_A}{1 - y_{A0}} = \left( \frac{1 - y_{As}}{1 - y_{A0}} \right)^{z/\delta} \)


4) Negligable Diffusion (Plug Flow)

\( W_{Az} = C_A U_z \)

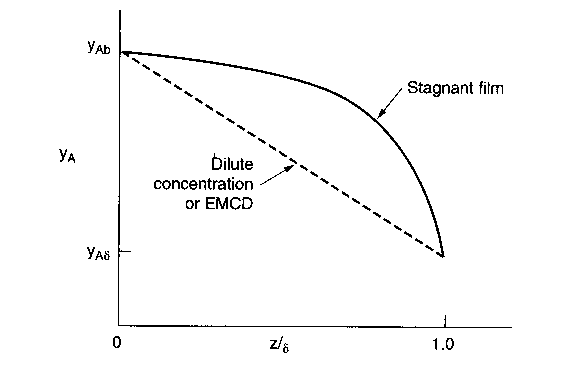
Plot of mole fraction yA versus dimensionless distance z over δ. The solid curve labeled 'Stagnant film' represents the actual concentration profile of species A, decreasing nonlinearly from yAb at z = 0 to yAs at z = δ. A dashed straight line labeled 'Dilute concentration or EMCD' connects yAb to yAs, representing the approximate linear profile under dilute conditions. Axes are labeled yA and z/δ, ranging from 0 to 1.

Example Relative Rates of Diffusional Transport
Example Measurement of Gas Phase Diffusivities
More Mole Balance with Diffusion and Reaction in 3-D
Example Measurement of Liquid Phase Diffusivities

Relative Rates of Diffusion and Reaction

Top
1.

Mole Balance on Species A at steady state

Diagram showing a fluid flow over a flat surface forming a boundary layer. Flow arrows enter from the left. The boundary layer grows along the surface, and species A diffuses vertically through it with a flux W_A. Horizontal lines are marked at z = 0, z, z + Δz, and z = δ, indicating the vertical extent of mass transfer.

\(\text{In} - \text{Out} + \text{Generation} = \text{Accumulation}\)

\(W_A A_c \big|_z - W_A A_c \big|_{z + \Delta z} + 0 = 0\)

\(\text{Divide by } A_c \text{ and take the limit as } \Delta z \to 0\)

\( \frac{dW_A}{dz} = 0 \)

Integrating:

WA=K'

2.

Rate Law / Constitutive Equation

Constitutive Equation

\( W_A = -cD_{AB} \frac{dy_A}{dz} + y_A (W_A + W_B) \)

\( \text{[EMCD: } W_A = -W_B \text{]} \)

\( W_A = -D_{AB} \frac{dC_A}{dz} \)

Rate Law on Surface

\( -r''_A = k'_A C_{AS} \)
3.

Boundary Conditions

Z=0 CA=CA0

Z=d CA=CA0

\( W_A = \frac{D_{AB}}{\delta} \left[ C_{A0} - C_{AS} \right] \)

The rate of arrival of molecules on the surface equals the rate of reaction on the surface.

\( W_A = -r''_A \)

\( W_A = \frac{D_{AB}}{\delta} \left[ C_{A0} - C_{AS} \right] = k_C \left[ C_{A0} - C_{AS} \right] \)

\( k_C = \frac{D_{AB}}{\delta} \)

kC is the mass transfer transfer coefficient. It can be found from a correlation for the Sherwood number:

\( \text{Sh} = \frac{k_C d}{D_{AB}} \)

which in turn is a function of the Reynolds Number

\( \text{Re} = \frac{\rho D V}{\mu} \)

and the Schmidt Number

\( \text{Sc} = \frac{\mu}{\rho D_{AB}} \)

For packed beds:

\( \text{Sh} = \left( \text{Re} \right)^{1/2} \text{Sc} \)

\( \frac{k_C d}{D_{AB}} \sim \left( \frac{D U}{\nu} \right)^{1/2} \)

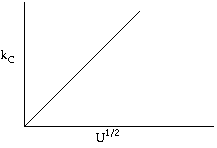
\( k_C \sim U^{1/2} \)

We see if we increased the velocity by a factor of 4, then the mass transfer coefficient, and hence the rate would increase by a factor of 2.

The flux to the surface is equal to the rate of reaction on the surface:

\( W_A = -r_A'' \)

\( k_C \left[ C_{A0} - C_{AS} \right] = k_r C_{AS} \)

\( C_{AS} = \frac{k_C}{k_r + k_C} C_{A0} \)

\( -r_A'' = \frac{k_C k_r C_{A0}}{k_r + k_C} \)

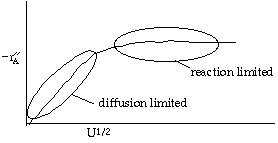
Let's look at the effect of increasing the velocity. We know that kc increases with increasing velocity, while kr is independent of velocity. At low velocities, the reaction is diffusion limited with kc >>kr and -rA=kc CAO

CASE 1

when kc >>> kr, then reaction is diffusion limited

\( C_{AS} \approx 0 \), rapid reaction on the surface, meaning that the overall reaction rate (\( W_A = k_C C_{A0} \)) is a function of velocity

\( -r_A' = k_r C_{A0} \)
CASE 2

when kc >>> kr, then reaction is reaction rate limited

\( C_{AS} \approx C_{A0} \), slow surface reaction, meaning that the overall reaction rate (WA=kr CAO) is independent of velocity

\( -r_A'' = k_r C_{AS} = \frac{k_r k_c}{k_r + k_c} C_{A0} \)
Graph showing a straight-line relationship between mass transfer coefficient kC and the square root of fluid velocity, U^1/2. The x-axis is labeled U^1/2 and the y-axis is labeled kC.

At high velocities, kc >> kr and -rA is independent of velocity

Graph showing the relationship between reaction rate -rA'' and the square root of velocity, U^1/2. The curve increases at first (labeled 'diffusion limited') and then levels off (labeled 'reaction limited'), indicating a transition from diffusion control to reaction control as velocity increases.



Mass Transfer in a Packed Bed of Catalyst Particles

Top

Diagram of a cylindrical packed bed reactor showing species A entering at catalyst weight W and exiting at W + ΔW. The shaded central region represents a differential reactor volume, and arrows labeled FA indicate molar flow rates of species A at both ends.

Mole Balance

\( \frac{dF_A}{dW} = r'_A \)

\( F_{A0} \frac{dX}{dW} = -r'_A \)

Rate Law / Constitutive Equation

\( -r'_A = -r''_A \, a_c \)

\( a_c = \left( \frac{6}{\rho_c d_p} \right) \) for single pellets

\( a_c = \left( \frac{6}{\rho_c d_p} \right) = \frac{6(1 - \phi)}{d_p} \) for packed beds

\( -r''_A = k_c [C_A - C_{AS}] \)

If

kr >>> kc

Then

\( -r''_A = k_c a_c C_A \)

\( F_{A0} = \frac{dX}{dW} = k_c a_c C_A = k_c a \, C_{A0} \frac{(1 - X)}{(1 + \epsilon X)} \frac{P}{P_0} \frac{T_0}{T} \)

We want to know how the mass transfer coefficient varies with the physical properties (e.g., DAB) and the system operating variables.

\( \text{Sh}' = (\text{Re}_e)^{1/2} \, \text{Sc}^{1/3} \)

\( k_C \sim d_p^{1/2} \, G^{1/2} \, D_{AB}^{2/3} \, \mu^{1/6} \, (1 - \phi)^{1/2} \, \phi^{-1} \, p^{-1/3} \)

\( a_c \sim d_p^{1/2} \)

\( D_{AB} \sim \frac{T^{7/4}}{P} \quad \mu \sim T^{1/2} \quad \text{(gas phase)} \)

\( \rho = \rho_0 \frac{T_0}{T} \left[ \frac{1}{1 + \epsilon X} \right] \frac{P}{P_0} \)

For isothermal operation, taking the rates for case 1 and case 2, the product of the mass transfer coefficient and the area acis

\( k_C \, a_{c2} = k_{C1} \, a_{c1} \left( \frac{P_1}{P_2} \right)^{1/3} \left( \frac{d_{P1}}{d_{P2}} \right)^{3/2} \left( \frac{G_2}{G_1} \right)^{1/2} \left( \frac{1 - \phi_2}{1 - \phi} \right)^{1/2} \left( \frac{\phi}{\phi_2} \right) \left( \frac{1}{1 + \varepsilon X} \right)^{1/3} \)

This equation tells us how the product of our mass transfer coefficient and surface area would change, if we were to change our operating conditions. In other words, it will help us answer "What if..." questions about our system.

For example: What effect does pressure drop have when all other variables remain the same?

\( k_C \, a_c = (k_C \, a_c)_0 \left( \frac{P_0}{P} \right)^{1/3} \)

For \( \varepsilon = 0 \):

\( \frac{P}{P_0} = \left( 1 - \alpha W \right)^{1/2} \)

Substituting:

\( k_C a_C = (k_C a_C)_0 (1 - \alpha W)^{1/6} \)

\( \frac{dX}{dW} = \frac{k_C a_C}{\nu_0} (1 - X)(1 - \alpha W)^{-1/6} \)

If

\( \alpha W \ll 1 \)

Then

\( X = 1 - e^{\frac{-k_C a_C W}{\nu_0}} \)
 

Shrinking Core Model

Top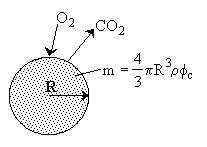

Diagram of a spherical particle of radius R undergoing combustion. Arrows show O₂ entering and CO₂ leaving the surface. The particle’s mass is given by m = (4/3)πR³ρϕc, where ρ is density and ϕc is a conversion factor.

\( \frac{dm}{dt} = r_c'' \cdot 4\pi R^2 \)

\( \frac{dR}{dt} = \frac{r_c''}{\phi_c \rho_c} \)

\( -r_c'' = -W_{Ar} = \frac{D_e C_{A0}}{R - \frac{R^2}{R_o}} \)

Time to complete consumption, tc

\( t_c = \frac{\rho_c R_o^2 \phi_c}{6 D_e C_{A0}} \)

Self Test WA=? for 2A<=>B
Self Test Comparing JA and BA for diffusion through a stagnant film
Self Test What 4 things are wrong with this solution?
Self Assess Object Assessment of Chapter 14
Sidenote Transdermal Drug Delivery

top