Chapter 14: External Diffusion Effects on Heteregeneous Reactions
Derivation
Diffusion through stagnant gas
Mole Balance
\( \frac{dW_{Az}}{dz} = 0 \)
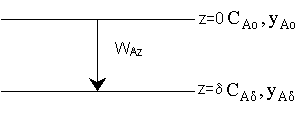
\( W_{Az} = K_1 \)
\( W_{Az} = -c D_{AB} \frac{dy_A}{dz} + y_A \left( W_{Az} + W_{Bz} \right) \)
Stagnant gas WBz = 0
\( W_{Az} = -c D_{AB} \frac{dy_A}{dz} + y_A \left( W_{Az} + 0 \right) \)
Rearranging
\( W_{Az} = \frac{-c D_{AB}}{1 - y_A} \frac{dy_A}{dz} = \frac{c D_{AB} d \ln(1 - y_A)}{dz} \)
\( W_{Az} = c D_{AB} \ln(1 - y_A) + K_2 \)
\( z = 0 \quad y_A = y_{A0} \)
\( K_2 = -c D_{AB} \ln(1 - y_{A0}) \)
\( z = \delta \quad y_A = y_{As} \)
\( K_1 \delta = c D_{AB} \ln(1 - y_{As}) - c D_{AB} \ln(1 - y_{A0}) \)
\( W_{Az} = K_1 \)
\( W_{Az} = \frac{c D_{AB}}{\delta} \ln\left( \frac{1 - y_{As}}{1 - y_{A0}} \right) \)
Concentration Profile
\( W_{Az} = c D_{AB} \frac{d \ln(1 - y_A)}{dz} = \frac{c D_{AB}}{\delta} \left( \frac{1 - y_{As}}{1 - y_{A0}} \right) \)
\( \frac{d \ln(1 - y_A)}{dz} = \left( \frac{1 - y_{As}}{1 - y_{A0}} \right) \)
\( z = 0 \quad y_A = y_{A0} \)
\( \ln(1 - y_{A0}) = \frac{z}{\delta} \ln\left( \frac{1 - y_{As}}{1 - y_{A0}} \right) + \ln(1 - y_{A0}) \)
\( \left( \frac{1 - y_A}{1 - y_{A0}} \right) = \left( \frac{1 - y_{As}}{1 - y_{A0}} \right)^{z/\delta} \)