Chapter 14: External Diffusion Effects on Heteregeneous Reactions
More on Mole Balance with Diffusion and Reactions in 3-D
We can also apply the mole balance of an element of value DxDyDz to obtain the variation of flow rates in three dimensions
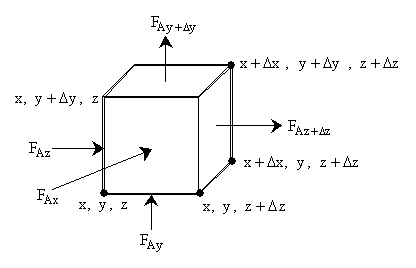
\( \left[ F_{Az} = W_{Az} \, \Delta x \, \Delta y \right] \)
\( \left[ \text{Molar Flow Rate In} \right] - \left[ \text{Molar Flow Rate Out} \right] + \left[ \text{Molar Flow Rate In} \right] - \left[ \text{Molar Flow Rate Out} \right] \)
\( \Delta x \Delta y W_{Az}\big|_z - \Delta x \Delta y W_{Az}\big|_{z+\Delta z} + \Delta x \Delta z W_{Ay}\big|_y - \Delta x \Delta z W_{Ay}\big|_{y+\Delta y} \)
\( \left[ \text{Molar Flow Rate In} \right] - \left[ \text{Molar Flow Rate Out} \right] + \left[ \text{Rate of Generation} \right] = \left[ \text{Rate of Accumulation} \right] \)
\( \Delta z \Delta y W_{Ax}\big|_x - \Delta z \Delta y W_{Ax}\big|_{x+\Delta x} + r_A \Delta x \Delta y \Delta z = \Delta x \Delta y \Delta z \frac{\partial C_A}{\partial t} \)
Dividing by DxDyDz and taking the limit as they go to zero
\( - \frac{\partial W_{Ax}}{\partial x} - \frac{\partial W_{Ay}}{\partial y} - \frac{\partial W_{Az}}{\partial z} + r_A = \frac{\partial C_A}{\partial t} \)
Equations for Figure
\( \begin{array}{cccc} F_{Ay+\Delta y} & \big| & x+\Delta x,\ y+\Delta y,\ z+\Delta z & \big| \ x,\ y+\Delta y,\ z \\ y+\Delta y,\ z+\Delta z & \big| & F_{Az} & \big| \ F_{Az+\Delta z} \ \big| \ F_{Ax} \\ x,\ y,\ z & \big| & F_z & \big| \ x+\Delta x,\ y,\ z+\Delta z & \big| \ x,\ y,\ z+\Delta z \end{array} \)