Chapter 14: External Diffusion Effects on Heteregeneous Reactions

Example: Measurement of Liquid Phase Diffusivities

A falling liquid jet is sometimes used to measure liquid-phase diffusivities of soluble gases. A jet of the pure liquid passes from a nozzle, designed to give a flat velocity profile, thence through a diffusion chamber containing the pure gas, and finally to a mixing vessel whose effluent is analyzed. For short jets it is usually a very good approximation to ignore curvature in the jet surfaces treating the process as diffusion into a fl at slab, since the concentration "boundary layer" is thin.

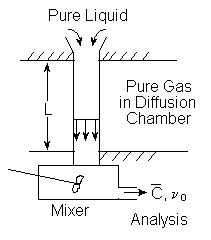
Diagram of a diffusion setup. Pure liquid evaporates into a vertical diffusion chamber filled with pure gas. The chamber has a height labeled L. Gas flows downward into a mixer, which leads to an analysis outlet where average concentration (C̄) and flow rate (ν₀) are measured.

a. Assuming a perfectly flat velocity profile, constant jet diameter and negligible longitudinal diffusion, use the well-known relation for unsteady diffusion into a planar slab to derive a relation between

\( \overline{C} \) = mixed outlet concentration at steady-state

C* = equilibrium concentration of gas in liquid at chamber pressure and temperature (constants)

n_o volumetric flow rate of jet

L jet length

D diffusivity of gas in liquid (D º D_AB)

b. In an experimental measurement of the diffusivity of CO₂ in water, the mixed outlet concentration of CO₂ is found to be

\( \overline{C} = 0.287 \times 10^{-6} \ \text{gm moles/cm}^3 \ \text{at } 25^\circ \text{C} \)

for a chamber pressure of 1 atmospheric CO₂, and a jet length of 3 cm., and a flow rate of 12.0 cm³ /sec of water. What is the corresponding value of the diffusivity of CO₂ in water?

c. Make an estimate of the maximum thickness of the CO₂ boundary layer, i.e., penetration depth. Is the assumption negligible surface curvature justified for a 1 mm diameter jet?

\( P_{CO_2} = H X_{CO_2}^* = 1640 \, X_{CO_2}^* \)

Liquid Jet

For small penetration depths, the cross-sectional area for radial diffusion is equal to the surface area of the jet

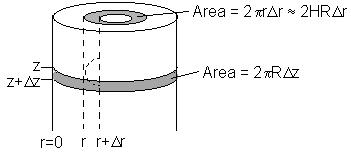
Diagram of a cylindrical shell element. The height ranges from z to z + Δz, and the radius ranges from r to r + Δr. The side surface area is labeled as approximately 2πΔr × H ≈ 2HΔr, and the bottom annular surface area is labeled as 2πRΔz.

\( 2\pi R \Delta r W_{Az}\big|_z + 2\pi R \Delta z W_{Ar}\big|_r - 2\pi R \Delta r W_{Az}\big|_{z + \Delta z} - 2\pi R \Delta z W_{Ar}\big|_{r + \Delta r} = 0 \)

¸ by 2pRDrDz and take the limit as Dz and Dr go to zero

\( -\frac{\partial W_{Ar}}{\partial r} - \frac{\partial W_A}{\partial z} = 0(1) \)

\( W_{Ar} = -D_{AB} \frac{\partial C_A}{\partial r} \)

\( W_{Az} = -D_{AB} \frac{\partial C_A}{\partial z} + y_A (W_{Az} + W_{Bz}) \)

\( W_{Ar} = -D_{AB} \frac{\partial C_A}{\partial r} + y_A \left( W_A + W_{B_A} \right) \quad \text{(small concentration of A)} \)

In the axial (i.e., z) direction, the convective molar flux, \( y_A \left( W_{Az} + W_{Bz} \right) \) will be much greater than the molar flux by molecular diffusion, J_A. One therefore can neglect J_Az with respect to \( y_A \left( W_{Az} + W_{Bz} \right) \).

\( W_{Az} \approx y_A (W_{Az} + W_{BC}) = y_A C V_z^* = C_A V = C_A U \quad (3) \)

Substitution of Equations (3) and (2) into Equation (1) yields the following partial differential equation:

\( \frac{\partial C_A}{\partial z} = \frac{D_{AB}}{V} \frac{\partial^2 C_A}{\partial r^2} \quad (4) \)

with the boundary conditions:

\( C_A = C_{A0} \quad r = 0 \quad Z > 0 \)

\( C_A = 0 \quad r > 0 \quad Z = 0 \)

\( C_A = 0 \quad r \to \infty \quad Z \geq 0 \)

\( \text{Let } h = \frac{r}{z^n} \)

\( \frac{D_{AB}}{V} \frac{\partial^2 C_A}{\partial \eta^2} \cdot \frac{1}{z^{2n}} = \frac{-n}{z} \eta \frac{\partial C_A}{\partial \eta} \)

z can be eliminated from this equation by setting n = 1/2

\( \frac{D_{AB}}{V} \frac{d^2 C_A}{d\eta^2} + \frac{\eta}{2} \frac{d C_A}{d\eta} = 0 \)

with the boundary conditions:

\( C_A = 0 \quad \text{as } \eta \to \infty \)

\( C_A = C_{A0} \quad \text{as } \eta \to 0 \)

\( \text{Let } P = \frac{dC_A}{d\eta} \quad \text{and } D_{AB} = D \)

\( \frac{dP}{d\eta} = -\frac{\eta}{2D/V} P \)

\( P = \frac{dC_A}{d\eta} = A \exp\left[ \frac{-\eta^2 V}{4 D_{AB}} \right] \)

\( C_A - C_{A0} = A \int_0^{\eta} \exp\left[ \frac{-\eta^2 V}{4 D_{AB}} \right] d\eta \)

\( \text{As } \eta \to \infty, \quad C_A \to 0 \)

\( A = -\frac{C_{A0}}{\int_0^{\infty} \exp\left( \frac{-\eta^2 V}{4D} \right) d\eta} \)

\( \frac{C_A - C_{A0}}{C_{A0}} = \frac{\int_0^{\eta} \exp\left( \frac{-\eta^2 V}{4D} \right) d\eta} {\int_0^{\infty} \exp\left( \frac{-\eta^2 V}{4D} \right) d\eta} \)

\( \text{Let } y = \frac{\eta}{\sqrt{4D/V}} \)

\( \frac{C_{A0} - C_A}{C_{A0}} = \frac{ \int_0^{\eta} \exp\left[ -y^2 \right] dy }{ \int_0^{\infty} \exp\left[ -y^2 \right] dy } = \frac{2}{\sqrt{\pi}} \int_0^{\frac{\eta}{\sqrt{4D/V}}} \exp\left[ -y^2 \right] dy = \operatorname{erf} \left( \frac{\eta}{\sqrt{4D/V}} \right) \)

\( \operatorname{erf}(X) = \frac{2}{\sqrt{\pi}} \int_0^X e^{-y^2} \, dy \)

\( \frac{C_A}{C_{A0}} = 1 - \operatorname{erf} \left( \frac{r}{\sqrt{4Dz/V}} \right) \)

\( \frac{C_A}{C_{A0}} = \operatorname{erfc} \left( \frac{r}{\sqrt{4Dz/V}} \right) \)

Total rate of mass transfer = N_Ar

\( N_{Ar} = 2 \pi R \int_0^L W_{Ar}\big|_{r=0} \, dz \)

\( W_{Ar}\big|_{r=0} = -D_{AB} \left. \frac{\partial C_A}{\partial r} \right|_{r=0} = C_{A0} \sqrt{ \frac{D_{AB} V z}{\pi z} } \exp\left[ \frac{-r^2 V}{4 D z} \right] \Big|_{r=0} \)

\( W_{Ar}\big|_{r=0} = \sqrt{ \frac{D_{AB} V}{\pi z} } \, C_{A0} \)

\( N_{Ar} = 2 \pi R \int_0^L \sqrt{ \frac{D_{AB} V}{\pi z} } \, dz = 4 R \sqrt{ D_{AB} V \pi L } \, C_{A0} \)

\( N_{Ar} = \overline{C}_A \, v_0 \)

\( \frac{ \overline{C} }{ C_{A0} } = 4 \sqrt{ \frac{D_{AB} L}{v_0} } \)

\( C_{A0} = \frac{P}{H} \, C_t = 3.35 \times 10^{-5} \, \text{gmole/cc} \)

P = pressure of CO₂ in the gas

H = Henry’s law constant

\( D_{AB} = \left( \frac{ \overline{C} }{ 4 C_{A0} } \right)^2 \frac{v_0}{L} \)

\( D_{AB} = \left( \frac{0.287 \times 10^{-6}}{4 \times 3.35 \times 10^{-5}} \right)^2 \cdot \frac{12}{3} \)

\( D_{AB} = 1.84 \times 10^{-5} \ \text{cm}^2/\text{sec} \)

\( \frac{C_A}{C_{A0}} = \operatorname{erfc} \left( \frac{r}{\sqrt{4 D z / V}} \right) \)

when C_A = 0.01 C_A0

\( 0.01 = \operatorname{erfc} \left( \frac{r}{\sqrt{4 D z / V}} \right) = \operatorname{erfc}(1.81) \)

r = d = thickness of the penetration zone

\( \delta = 1.81 \sqrt{ \frac{4 D_{AB} z}{V} } = 1.81 \sqrt{ \frac{4 D_{AB} L}{V} } = 1.81 R \sqrt{ \frac{4 D_{AB} \pi}{\pi R^2 V} } \)

\( \frac{\delta}{R} = 1.81 \sqrt{ \frac{4 D_{AB} \pi L}{Q} } = 6.7 \times 10^{-3} \)

d = 0.67 ´ 10^–2mm or 1.3 percent of the radius; therefore, assumption of short penetration depths is justified.

Rather than using one experimental point to determine the diffusivity, one may vary the jet length to obtain a series experimental points. The total amount of CO₂ absorbed is

\( \overline{C} = C_{A0} \cdot 4 \sqrt{ \frac{D_{AB} L}{v_0} } \)

\( W = 4 C_{A0} \sqrt{ D_{AB} L v_0 } \)

A plot of N_Ar vs.\( \sqrt{L} \) should be a straight line of slope

\( S = 4 C_{A0} \sqrt{v_0} \sqrt{D_{AB}} \)

\( D_{AB} = \frac{S^2}{16 \, C_{A0}^2 \, v_0} \)

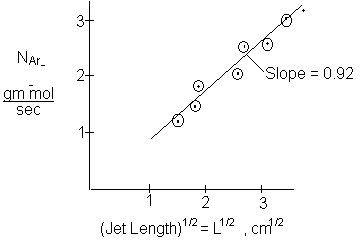
Graph plotting N_Ar (in gm-mol/sec) on the y-axis versus the square root of jet length, L^1/2, in cm^1/2 on the x-axis. Data points form a linear trend with a best-fit line labeled 'Slope = 0.92'.

From the data of W. J. Thomas in J. Applied Chem.,17, p. 350 (1967)

\( D_{AB} \text{ at } 25^\circ \text{C} = 1.95 \times 10^{-5} \ \text{cm}^2/\text{sec} \)

Return to Chapter