Chapter 14: External Diffusion Effects on Heteregeneous Reactions

Self Test: Comparing JA and BA for diffusion through a stagnant film

WA = JA + WA

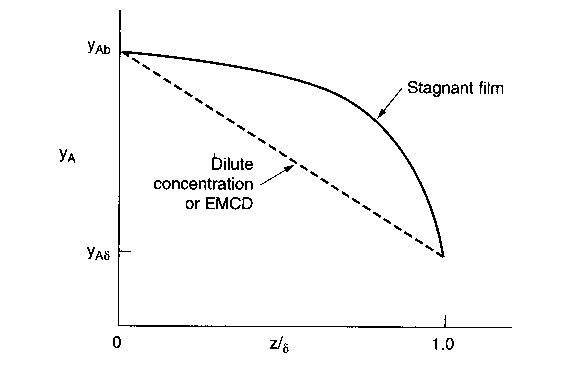
Graph of mole fraction yA versus dimensionless distance z over δ. The solid curve labeled 'Stagnant film' shows a nonlinear decrease from yAb at z=0 to yAs at z=δ. A dashed straight line represents the 'Dilute concentration or EMCD' approximation connecting the same endpoints. y-axis is labeled yA, and x-axis is labeled z/δ ranging from 0 to 1.0.

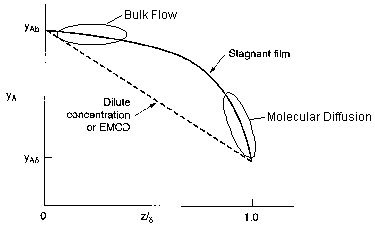
Concentration Profiles \( (y_{AS} \equiv y_{AS}) \)

\(\text{EMCD:} \quad \frac{y_{A0} - y_A}{y_{A0} - y_{AS}} = \frac{z}{\delta} \)

\(\text{Stagnant Film:} \quad \frac{1 - y_A}{1 - y_{A0}} = \left( \frac{1 - y_{AS}}{1 - y_{A0}} \right)^{z / \delta} \)

Fluxes

\(\text{EMCD:} \quad W_{Az} = \frac{c D_{AB}}{\delta} \left[ y_{A0} - y_{AS} \right] \)

\(\text{Stagnant Film:} \quad W_{Az} = \frac{c D_{AB}}{\delta} \ln \left( \frac{1 - y_{AS}}{1 - y_{A0}} \right) \)

In what regions (i.e., z/d) does JA dominate and in what regions does BA dominate?

Go to Solution





















































Solution

\( W_A = J_A + B_A \)

\( \boxed{ \text{Ratio} = \frac{J_A}{B_A} } \)

\( B_A = y_A W_A \)

\( J_A = -c D_{AB} \frac{\partial y_A}{\partial z} \)

also

\( J_A = W_A - B_A = W_A (1 - y_A) \)

\( \text{Ratio} = \frac{W_A (1 - y_A)}{W_A y_A} \)

\( \text{Ratio} = \frac{1 - y_A}{y_A} \)

when yA ~ 1 Ratio ~ 0 Bulk Flow Dominates

yA ~ 1 Molecular Diffusion Dominates

yA

Ratio

1

0.9

0.75

0.5

0.25

0.10

0

0

0.11

0.33

1

3

9

\( \infty \)

Graph of R versus yA0, showing a decreasing curve. R starts high when yA0 is near 0 and gradually decreases as yA0 approaches 1. The x-axis is labeled yA0 and ranges from 0 to 1, and the y-axis is labeled R.
Graph showing mole fraction yA versus dimensionless distance z/δ. The curve labeled 'Stagnant film' decreases nonlinearly from yAb to yAs. Ellipses highlight 'Bulk Flow' near the top and 'Molecular Diffusion' near the bottom. A dashed line labeled 'Dilute concentration or EMCD' connects yAb to yAs linearly. x-axis is labeled z/δ, and y-axis is labeled yA.



Back to Chapter