Chapter 14: External Diffusion Effects on Heteregeneous Reactions

Example: Measurement of Gas Phase Diffusivities

Consider the test tube partially filled with a volatile liquid shown below.

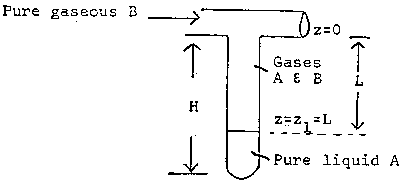
Schematic of a vertical tube setup. Pure gaseous B enters horizontally at the top where z = 0. The tube turns downward and contains gases A and B in the vertical section. At depth L (z = z1 = L), there is pure liquid A. The height of the vertical gas region is labeled L, and the full tube height is labeled H.

A mass balance on A in the gas phase gives

\( -\left( \frac{\partial W_A}{\partial z} \right)_t = \left( \frac{\partial C_A}{\partial t} \right)_z \)

Using the quasi-state assumption that the concentration at each point z changes very slowly with time,

\( \left( \frac{\partial C_A}{\partial t} \right)_z \approx 0 \)

Then

\( \frac{dW_A}{dz} = 0 \)

Integrating WA = Number which is independent of distance, z, but is a function of time, t

WA = f(t)

For diffusion of A through a stagnant gas

\( W_B = 0 \)

\( W_A = \frac{-c D_{AB}}{1 - y_A} \frac{\partial y_A}{\partial z} \)

at \( z = 0 \quad y_A = y_{A2} = 0 \)

\( z = z_o = L \quad y_A = y_{A1} = \frac{P_V}{P_T} \)

where PV = vapor pressure and PT = total pressure

Since NA is independent of z under the quasi-steady assumption, the above differential equation can be integrated to give

\( y_A = 1 - (1 - y_{A1}) \left[ \frac{1}{1 - y_{A1}} \right]^{\frac{L - z}{L}} \)

Then

\( W_A = \frac{c D_{AB}}{L(t)} \ln\left( \frac{P_T}{P_T - P_V} \right) \)

For constant temperature and pressure, C = total concentration = a constant = \( \left( \frac{P_T}{R T} \right) \). Only the distance between the top of the capillary and the gas-liquid interface is varying.

Overall balance on the entire system

IN − OUT = ACCUMULATION

\( 0 - W_A A = \frac{d}{dt} \left( \rho_g A L + \rho_\ell A (H - L) \right) \)

\( W_A = \rho_\ell \left[ 1 - \frac{\rho_g}{\rho_\ell} \right] \frac{dL}{dt} \quad , \quad \rho_\ell = \text{molar density of liquid} \)

\( \rho_g = C \cdot \text{molecular weight} \)

\( \frac{\rho_g}{\rho_\ell} \ll 1 \)

\( W_A = \frac{c D_{AB}}{L} \ln \left( \frac{P_T}{P_T - P_V} \right) = \rho_\ell \frac{dL}{dt} \)

Initial conditions: t = 0 , L = Lo

Integrating

\( L^2 - L_0^2 = \left[ \frac{2 D_{AB} C}{\rho_\ell} \ln\left( \frac{P_T}{P_T - P_V} \right) \right]^t t \)

Rearranging:

\( \frac{t}{(L - L_0)} = \frac{\rho_\ell}{2 D_{AB} C \ln\left( \frac{P_T}{P_T - P_V} \right)} (L - L_0) + \frac{L_0 \rho_\ell}{D_{AB} C \ln\left( \frac{P_T}{P_T - P_V} \right)} \)

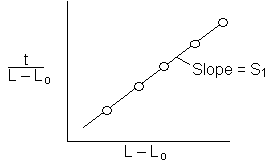
Graph of t divided by (L minus L₀) on the y-axis versus (L minus L₀) on the x-axis. Data points form a straight line with a positive slope labeled S₁.

The height of the gas-liquid interface, L, can easily be measured with a cathetometer. A plot at t/L–Lo vs. (L–Lo) should yield a straight line of slope S from which the diffusivity can be calculated from the equation

\( D_{AB} = \frac{\rho_\ell}{2 S_1 C \ln\left( \frac{P_T}{P_T - P_V} \right)} \)


Return to Chapter