Patterns and morphology in biology
The two central questions in developmental biology are: how is a cell informed of its position in a developing organism, and how does an organ gain information of its size? The first question is relevant to the execution of a genetic program that, for instance, fixes the color of a cell in the iris. The genetic code carries the instructions, but in order to execute the correct version of it, positional information has to be relayed. The second question is relevant to attainment of terminal size of an organ. It is not difficult to argue that this information can come either from a diffusing field, or from mechanics. These are the only physical phenomena accesible to the developing organism that convey position and spatial scale. For this reason, the study of patterning via reaction diffusion equations, and development of morphology via elastic instabilities has been of interest in soft matter physics for decades. In this work we study a broad family of equations for reaction, transport and elasticity, which separately or in combination, can dictate the formation of patterns on leaves, flowers, insect wings and animal skins, as well as the morphology of finger prints, the highly folded structure of the intestine and brain, the development of features such as on the face, the form of molluskan shells, and packing of cells in the early embryo. Our recent work on molluskan shells is a joint study with Computational Physics Group alumnus Shiva Rudraraju, Oxford mathematicians Derek Moulton and Alain Goriely, and biologist Regis Chirat. The model of intestinal folding is joint work with developmental biologist Deborah Gumucio and mathematical biologist Santiago Schnell.
- Papers:
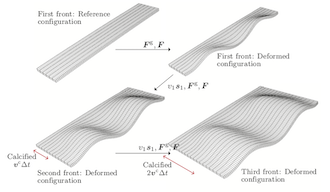
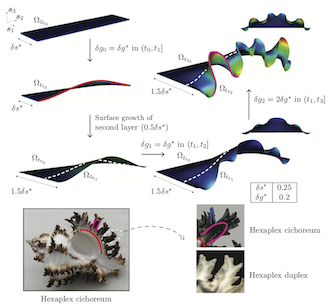
- A computational framework for the morpho-elastic development of molluskan shells by surface and volume growth
S. Rudraraju, D.E. Moulton, R. Chirat, A. Goriely, K. Garikipati
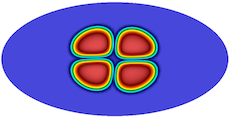
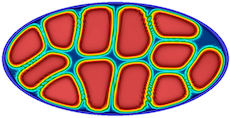
[available on arXiv]- A diffuse interface framework for modelling the evolution of multi-cell aggregates as a soft packing problem due to growth and division of cells
J. Jiang, S. Rudraraju, K. Garikipati
[available on arXiv]- A computational study of the mechanisms growth-driven folding patterns on shells, with application to the developing brain
S.N. Verner, K. Garikipati
Extreme Mechanics Letters
Vol. 18: 58-69, January 2018, doi.org/10.1016/j.eml.2017.11.003
[available on arXiv]- Perspectives on the mathematics of biological patterning and morphogenesis
K. Garikipati
Journal of the Mechanics and Physics of Solids
Vol. 99: 192-210, 2017, doi:10.1016/j.jmps.2016.11.013
[available on arXiv]- Coordination of signaling and tissue mechanics during morphogenesis of murine intestinal villi: a role for mitotic cell rounding
A.M. Freddo, S.K. Shoffner, Y. Shao, K. Taniguchi, A. S. Grosse, M.N. Guysinger, S. Wang, S. Rudraraju, B. Margolis, K. Garikipati, S. Schnell and D.L. Gumucio
Integrative Biology
Vol. 8: 918-928, 2016, doi:10.1039/C6IB00046K
A number of examples follow, showing the development of patterns and morphology by a combination of reaction-diffusion, phase segregation and elastic instabilities.

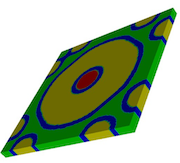
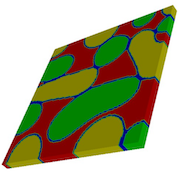
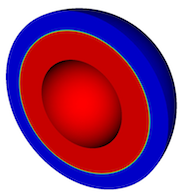
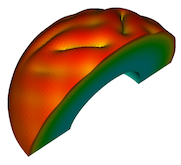
[Click images to enlarge/play. Videos best viewed at full-screen setting.]