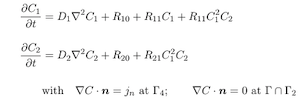Computational Physics Group

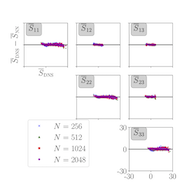
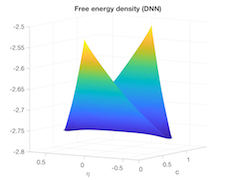
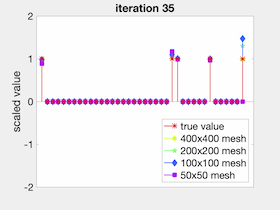
A cornerstone of computational models for phase-transformig materials is the class of first-order dynamics equations called phase-field methods, including the widely used Cahn-Hilliard and Allen-Cahn models. Phase-field methods may be regarded as imposing first-order dynamics to traverse a free energy landscape in search of equilibrium configurations, and lead to fascinating evolving patterns, which we, and others, have studied. However, if we are interested only in the equilibrium states, there may be alternative approaches to the phase-field dynamics, which could get trapped in very slow regimes, or have to struggle through stiff responses of the numerical solution. Instead, we have forged a combination of machine learning techniques including surrogate optimization, multi-fidelity modelling and sensitivity analysis as an alternative to phase field dynamics to compute precipitate morpholgies in a phase separating alloy. As we show, not only can machine learning approaches prove successful at finding the corresponding minima, but the resulting workflows naturally leverage heterogeneous computing architectures, which deliver efficiencies in terms of raw FLOP counts.

Papers:

Machine learning materials physics: Surrogate optimization and multi-fidelity algorithms predict precipitate morphology in an alternative to phase field dynamics
G. Teichert, K. Garikipati
Computer Methods in Applied Mechanics and Engineering
October 2018, doi.org/10.1016/j.cma.2018.10.025
[available on arXiv]

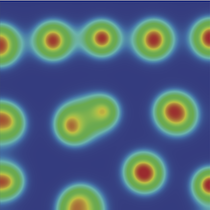
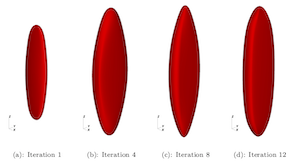
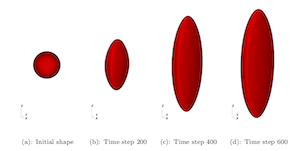
Shown here are comparisons of precipitate morphologies computed with the machine learning methods (left) and phase-field dynamics (right)

[Click images to enlarge

The problem of modelling the effective response that arises from a microstructure, without explicitly representing it, is common to a range of physics phenomena, and is referred to as homogenization. While there is a vast mathematical literature of analytic and semi-analytic methods on this subejct, there remain challenges with complex, if ordered, microstructures, and moreso for random ones. In this work we are interested in the homogenized, nonlinear elastic response of microstructures created by martensitic phase transformations in materials, and for the reasons just explained, we choose to take a numerical, rather than analytic approach to homogenization. We first generate a small number of periodic, martensitic microstructures using a gradient-coercified model of non-convex elasticity at finite strain, using our unique computational framework for that very challenging problem. We next subject a chosen martensitic microstructure to a large number (~3000) strain states and compute the elastic response at high-fidelity. This is our data generation step by direct numerical simulation. We then train deep neural networks (DNNs) on the homogenized response from these data. Remarkably, we train against the free energy data, but demonstrate that the (derivative) stress-strain response is obtained at high-fidelity from the DNN. This is a first step toward also allowing microstructures to vary between samples.

Papers:

Machine learning materials physics: Deep neural networks trained on elastic free energy data from martensitic microstructures predict homogenized stress fields with high accuracy
K. Sagiyama, K. Garikipati
[available on arXiv]

Shown are a microstructure and a validation of its homogenized, nonlinear, stress-strain response derived from a DNN trained on free energies, only

[Click images to enlarge/play]

The physics of a material can be described at multiple scales - from atomic to micro to macro. The phenomena ocurring at small scales can inform the behavior of the material at larger scales. For example, many models at the continuum level rely on a description of the material's free energy. Although free energy data is not generally found directly, its derivatives can be found using models at the atomic scale. To bridge these scales, we created an Integrable Deep Neural Network (IDNN). An IDNN can be trained to (partial) derivative data, then analytically integrated to recover an accurate representation of the free energy. This DNN representation of the free energy can be used as input to continuum level simulations, such as phase field dynamics. Thus, the information that the IDNN learns from the atomic scale data is used to drive the physics at the continuum scale.

Papers:

Machine learning materials physics: Integrable deep neural networks enable scale bridging by learning free energy functions
G.H. Teichert, A.R. Natarajan, A. Van der Ven, K. Garikipati
[available on arXiv]

Shown here are an example free energy density surface as represented by a DNN (left) and the microstructure it predicts with phase-field dynamics (right)

[Click images to enlarge

The widespread use of sensors, high throughput experiments and simulations, as well high performance computing have made ``big data'' available for a range of engineering physics systems. This sparked an explosion of interest in data-driven modeling for these systems. An extreme manifestation of this still-developing field is seen in ``model-free'' approaches that do not rely on physics-based knowledge. While holding promise of very high computational efficiency, such a path to modelling draws criticism for its ``black box'' nature and often lack of interpretability, and more seriously, offering scant openings for analysis when the model fails. The availability of data that is abundant (in some sense that changes with the system) also presents opportunities to discover mathematical forms of the underlying behavior that have well-understood physical meaning. This is the field of system identification, which is particularly compelling for determining the governing partial differential equations (PDEs). This is so, because knowledge of the PDE directly translates to deep insights to the physics, guided by differential and integral calculus.

Papers:

Variational system identification of the partial differential equations governing pattern-forming physics: Inference under varying fidelity and noise
Z. Wang, X. Huan, K. Garikipati
[available on arXiv]

Shown here are an example of identifying the coupled diffusion-reaction equations for two species following Schnakenberg kinetic(middle plot), by stepwise regression (right plot).

[Click images to enlarge