Computational Physics Group

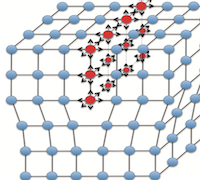
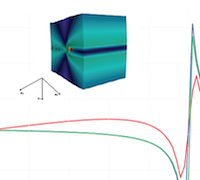
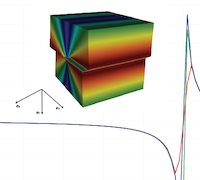
Classical elasticity is scale invariant: it does not admit length scales intrinsic to the material. The only length scale which may manifest itself arises from the problem geometry. However, real materials do posses intrinsic length scales (i.e., interatomic distance, dislocation cells, grain sizes, etc). If the deformation varies on these scales, size effects may arise. They mollify singularities that otherwise appear, for instance in classical elastic descriptions of defects such as cracks, point defects, dislocations and grain boundaries. They also arise as essential elements to the formation of strain­driven microstructure, such as twinning in HCP metals. One framework that is appropriate for treating such problems is the strain gradient formulation of elasticity, which is a natural extension of classical elasticity by a Taylor series expansion of the deformation map to include gradients of strain. We have developed a comprehensive numerical framework for Toupin’s theory of nonlinear gradient elasticity and obtained the first complete three-dimensional numerical solutions to a broad range of boundary value problems in gradient elasticity at finite strain. The governing equation is a fourth order partial differential equation with boundary conditions that extend to couple-stresses, line loads as well as Dirichlet conditions on normal strains, in addition to the standard ones on displacement and traction. Studies conducted using the framework include gradient length scale effects on microscale/nanoscale structural problems, regularization of crack tip solutions and modeling of mechanically induced microstructure.

Publications:

Three dimensional iso-geometric solutions to general boundary value problems of Toupin's theory of gradient elasticity at finite strains
S. Rudraraju, A. Van der Ven, K. Garikipati
Computer Methods in Applied Mechanics and Engineering
Vol 278: 705-728, 2014
available on arXiv

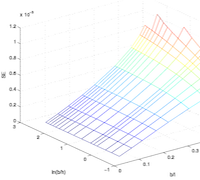
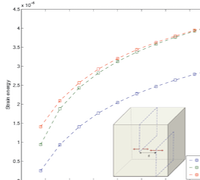
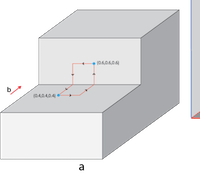
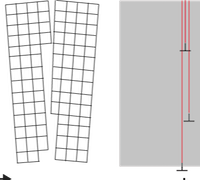
Shown here are the PDE, C1 continuous basis functions, comparison of analytical and numerical solutions in 1D, optimal convergence of error norms, 3D BVP's involving beam torsion, line load, crack and microstructure.

[Click images to enlarge/play]

We also have applied the framework to studying defect fields near cores based on a novel representation of point defects and dislocations as arrangements of force dipoles. The proper continuum description is in the theory of distributions. Remarkably, the variational setting allows a high-fidelity representation of these fields that can be realized with finite element and isogeometric methods. In ongoing work we are exploring the extraction of the dipole tensor by comparison with density functional theory calculations of defect configurations. Another front on which we see potential for our approach is in computations involving large numbers of interacting defects.

Publications:

A three dimensional field formulation, and isogeometric solutions to point and line defects using Toupin's theory of gradient elasticity at finite strains
Z, Wang, S. Rudraraju, K. Garikipati
Journal of the Mechanics and Physics of Solids
Vol. 94: 336-361, 2016, doi:10.1016/j.jmps.2016.03.028
[available on arXiv]

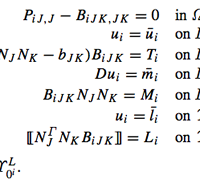
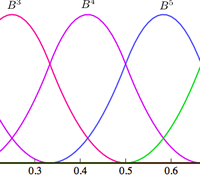
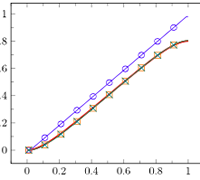
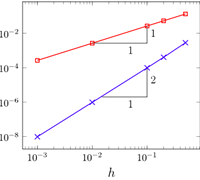
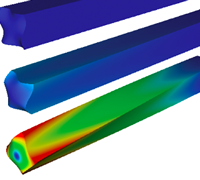
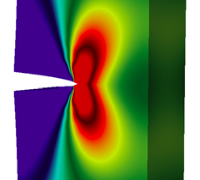
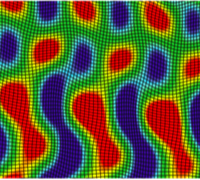
[Click images to enlarge/play]