
The article is the second of three parts covering Dr. Alan Stern’s lecture on the discovery of Kuiper belt objects (KBOs) and their importance in the Solar System.
In the previous article [“Pluto and the Three-Zoned Solar System,” by Douglas Warshow, May 2009], we saw how the KBOs form a numerically significant portion of our planetary system. Can the Kuiper belt tell us anything else about the Solar System?
Continuous study of the Kuiper belt shows that it possesses a dynamically complex system. In spite of the large average distance between any two KBOs, the occasional close encounters render any long-range orbital predictions useless. Any slight error in determining an object’s position and/or velocity would eventually lead to vastly different results. Sure the KBOs are relatively small and (for the most part) far away from each other, but there are thousands of them and even small effects can add up given enough time.
There are, however, some KBOs that do have predictable orbits. As an example, there are a number of them that orbit the Sun twice for every two times that Neptune completes one orbit. These particular objects are said to be in 2:3 orbital resonance with Neptune. (Incidentally, Pluto happens to be one of these objects.)
Now, before proceeding further, let me first present a small primer on one of the most abused concepts in orbital mechanics: the slingshot effect (otherwise known as gravity assist).
You may have either read or seen some instance in a “space opera” where the main character’s ship is in orbit about some distant world. Some emergency then occurs, so the hero quickly responds by having his/her ship dive close to the planet’s surface. Their “reason” for doing this is to increase speed so that they employ the “slingshot effect” to accelerate the ship to an incredible (literally) speed and break orbit. The hero then proceeds to save the day. And all of this takes place without using a drop of fuel.
Sorry, Defenders of Galactic Freedom, that’s not how it works.
What the hero (and the author, I might add) does not seem to realize is that gravity never stops acting on the ship, no matter how fast the ship is moving. The same force that accelerates the ship on the inbound leg also decelerates the ship on the outbound portion.


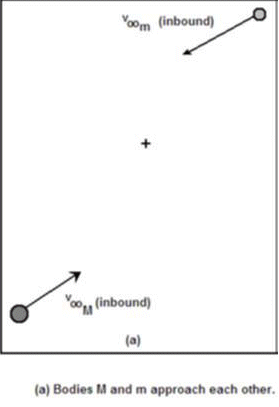
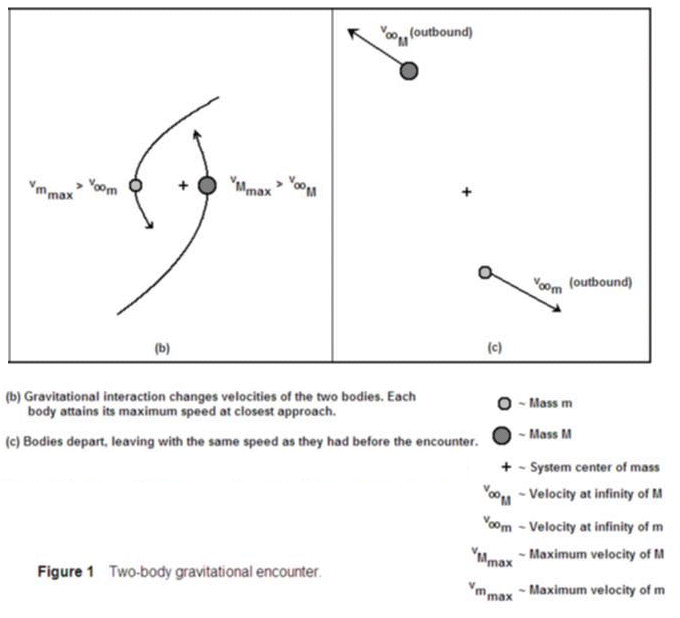
Consider the scenario in Figure 1(a). Two bodies having masses M and m are moving through space with velocities v∞M and v∞m, respectively, relative to the system’s center of mass*. (The infinity symbol indicates that the body is far enough away for its velocity not to be significantly influenced by the gravitational field of any other mass.) As long as the velocities are not pointed directly at the center of mass, the bodies will accelerate until they reach their maximum velocities, vMmax and vmmax, when they are at their minimum separation [Figure 1(b)]. Figure 1(c), shows (as described earlier), the bodies heading away from each other with the same speeds they possessed before they first encountered each other. Only their directions have changed.
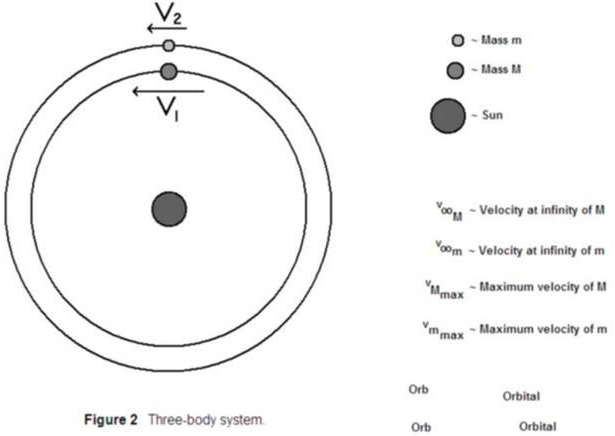
How then does the slingshot effect actually work? The answer is to bring in a third body. Figure (2) shows M and m orbiting a more massive body—we’ll call it the Sun to simplify matters. The body that orbits closer to the Sun will have the greater orbital velocity. Notice, in this case, that M and m revolve about the Sun; they do not revolve about each other. This means that the only base velocity they share is that of the Sun. The actual shapes of the respective orbits do not matter for qualitative purposes.
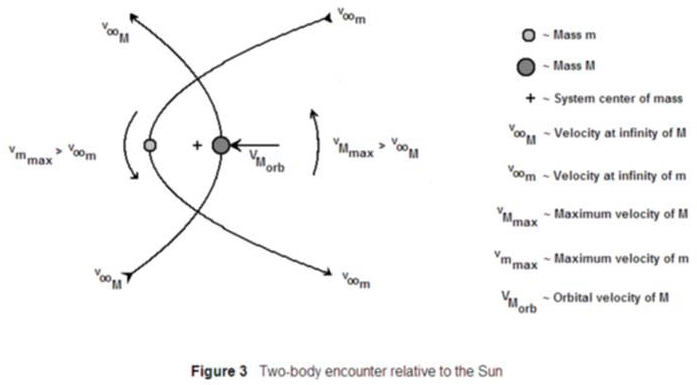
Now examine Figure 3. It is generally the same as the combination of Figures 1(a), (b) and (c); but with one important addition: the orbital velocity of M (vMOrb). If we were watching this encounter while floating with the center of mass, the paths would look exactly the same as in the case depicted in Figure 1. But since the center of mass is moving with relative to the Sun, we must add the system’s velocity to the others. If M has a much greater mass than m (which we shall assume for the rest of this article), the system’s orbital velocity is essentially the same as vMOrb. This velocity will be added to v∞m to arrive at a different outbound velocity.
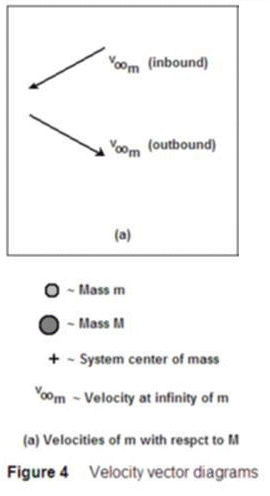
Figure 4 shows the above two scenarios in terms of velocity vectors. Figure 4(a) shows the inbound velocities of v∞m described in Figure (1). As before, only the direction has changed.
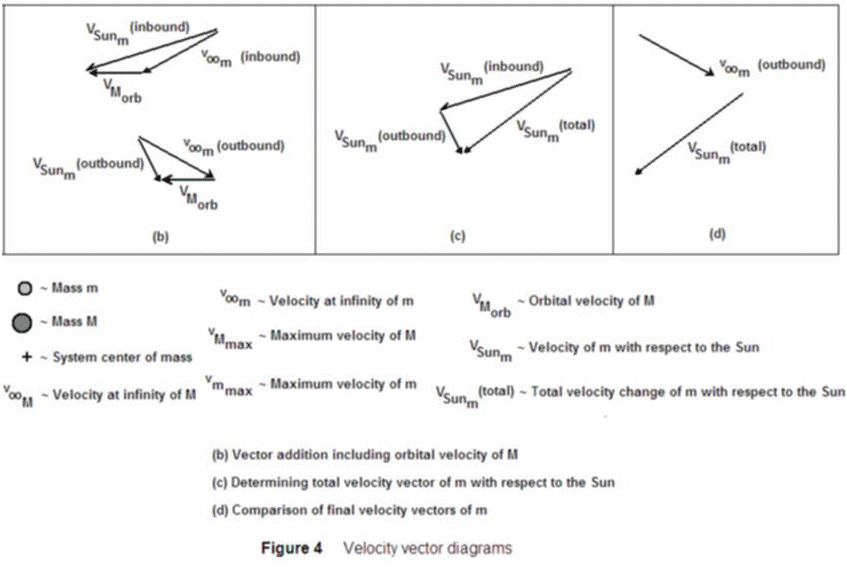
Figure 4(b) shows how adding** vMOrb to v∞m creates the inbound and outbound vectors of m relative to the Sun [VSunm(inbound) and VSunm(outbound), respectively]. The final result, VSunm(total), is shown in Figure 4(c). Figure 4(d) shows a comparison of vectors v∞m and VSunm(total). Notice that VSunm(total) is the longer of the two. This is how the slingshot effect truly works.
Two factors that determine the velocity change are the angle of approach of m (with respect to M) and how deep into M’s gravity well m enters. For instance, if m approached M practically head on and M’s gravity caused m’s path to turn 180°, m’s new heliocentric velocity would be vMOrb plus two times v∞m. Similarly, if m approached from M’s trailing end, m’s new heliocentric velocity would only be vMOrb - v∞m.
Another important aspect of the slingshot effect: it does not actually provide a “free” boost; the increase in velocity of m comes at a cost of a proportional decrease in the velocity of M. Since the proportion is m/M and, as stated earlier, we’re assuming that M >> m, the cost will be small. But it is not zero; this will be important later.
And now, back to our featured discussion.
Orbital resonance can have one of two effects on the less massive of two bodies experiencing it. First let’s look at Jupiter and the asteroid belt. While you might think that the asteroid belt has basically smooth distribution of bodies within its region, there exist a number of gaps, almost akin to the Cassini division in Saturn’s rings. (The Cassini division, though, is formed due to a different arrangement.) These depopulated areas are named Kirkwood gaps after their discoverer.
The Kirkwood gaps are created by Jupiter in the manner illustrated in Figure 4, though with Jupiter in the outer orbit. Normally each asteroid would only acquire a minor velocity boost from Jupiter. The Kirkwood gaps, however, mark the orbital regions that are in a particular resonance with Jupiter (2:1, 3:2, 3:1, etc.). So as they orbit, asteroids which start in those areas will receive repeated boosts from Jupiter at the same locations. Over time, the asteroid’s orbit becomes more and more eccentric (i. e., elliptical) until the asteroid leaves the region altogether.
Pluto, however, resides in a 2:3-resonant orbit with Neptune and has obviously not been ejected. How come? As you’ll see in Figure 5, Pluto is in an elliptical orbit (plus it is inclined with respect to the plane of the ecliptic) and is positioned such that it never receives increasing boosts from Neptune. As a matter of fact, any perturbations Pluto might receive would be corrected by Neptune gravitational influence. So, in a sense, Pluto is “locked” into this relation with Neptune. I suppose one could refer to it as an ”anti-boost” resonant orbit.
Okay, you may be wondering, but what has all this to do with KBOs? Well, astronomers have found that the Kuiper belt is also non-uniform in its member distribution but, unlike the asteroid belt, the orbits that are resonant with Neptune are regions of clustered bodies, not of depopulation.
To figure out what would cause this scenario, several astronomers have run what are called Nbody simulations; these are computer programs that calculate the velocities and distribution of multiple numbers of masses over time. (The “N” refers to some general number of bodies in the simulation.) In these simulations, the astronomers wanted to see what the effects on the KBOs would be if Neptune migrated away from the Sun. The result: as Neptune moved outward it actually collected KBOs in its resonant orbits and “pumped up” their respective eccentricities. By examining the degree of “pumping” at the 3:2 resonant orbit, the astronomers determined that Neptune’s must have originally started off 9 AUs closer to the Sun than its present position. That difference is almost the same distance as from the Sun to Saturn.
So what would cause Neptune to migrate outwards?
According to theoretical any computer models, the early Solar System formed by the collapse of a proto-planetary nebula. Over the course of time, the nebula’s gas and dust accreted to form larger clumps of matter called planetesimals. Although the majority of these worlds themselves accreted to become the planets, far more of them remained than the current sum of asteroids, comets and KBOs. The models did predict the existence of planetesimals beyond Neptune’s orbit, but only in orbits that were nearly circular; these results run counter to observational evidence.
New models were created that took into account the planetesimals’ gravitational influence on the planets. The results showed than when (on average) planetesimals possessed an angular momentum component perpendicular to the orbital plane greater than that of a planet, the planet would migrate outward. Similarly, when said component was less than that a planet, that planet would migrate inward. In fact, the models depicted the outward migration of Neptune, Uranus and Saturn and the inward migration of Jupiter.
The new models also show the cause of the non-circularity of the KBO orbits. As in the case of Pluto, Neptune can occasionally “lock” a body which is an orbit resonant with that of Neptune. As Neptune migrated outward, its resonant “zones” crossed the orbits of more planetesimals, some of which were also carried outward. (This process is called resonant dragging.) While this space regatta went sailing outward, resonance with Neptune kept adding energy to the captured bodies and, thus, increased their respective eccentricities. Since different planetesimals entered the different resonant zones at different times, a wide range of orbital shapes would be the outcome.
So the current KBO orbits act as “fossil” evidence for the past migration of the gas giant worlds. Once again the supposedly insignificant bodies have given astronomers a new view of the Solar system.
I should note, however, that a new puzzle has arisen from these simulations: the models predict that Neptune should have migrated farther than is evident. Apparently some depletion occurred at a distance of about 30 AUs from the Sun. No plausible explanation has been given as yet.
Next time: Alan Stern’s discussion of Pluto, KBOs and their roles in regard to the controversial term “planet.”
Note: Many thanks again to John Causland for providing me with a DVD of Dr. Sterns’ lecture.
*In describing or analyzing a system of particles, it is always easiest to use the system’s center of mass as the reference point. In a two particle system, if one particle has a non-zero velocity with respect to the center of mass, then so must the other in order to balance the system.
**To add vectors, just place them together point to tip, without changing their lengths or orientations. Their sum is a vector that begins at the tip of the first vector and ends at the point of the last one.
[ See also part 3, “Pluto, KBOs and the Definition of “Planet”,” by Douglas Warshow, November, 2009 ]