

The next time you look up at the night sky, consider this: everything you see is moving. We’ve known for thousands of years that planets move. More recently we discovered that stars move; there are galaxies and they move as well. Gravity explains most of that motion (most but not all).
In the beginning Astronomy was only a means to predict planetary motions. The first predictions were made with mechanical devices—they weren’t very accurate, but the accuracy slowly improved. Eventually mechanical devices were replaced with mathematical equations. Only equations allowed enough accuracy for Astronomy to become a true science. In this article I will attempt to give a broad outline of how this happened (a complete description would require many equations and many pages, I’m not going to attempt that—if you really want to see equations, see the references).
I talked about General Relativity in Part 1 of this article. General Relativity is the most accurate theory of gravity we have, but it is much harder to use than Newton’s Theory of Gravity. For that reason Newton’s Theory is used for astronomical calculations in most cases. This is the story of how Newton’s Theory was developed.
People have known for a long time that planets move, and have been able to make rough predictions, but precise predictions were impossible until Johannes Kepler. In the early 1600’s Kepler studied the motion of Mars—after eight years of hard work he produced what we now call Kepler’s equation, it showed the planets orbit the sun in ellipses and they move faster when close to the sun—slower when farther from the sun. Similarly people had a rough understanding of how apples and other objects fall to the earth, but Galileo Galilei was the first person to collect data on falling objects (actually balls rolling down a sloped platform). From these data he produced an equation that showed falling objects travel in parabolas.


While the work of Galileo and Kepler were significant achievements, they left open questions. No one knew how to predict the arrival or motion of a comet. In addition, neither man seemed to make the connection between the motion of the falling apple and the motion of the planets (they were considered to be two different phenomenon with two different equations). Nor could they explain why apples or planets move the way they did (Galileo viewed Kepler as a rival, and the two did not work together even though they were working on somewhat similar problems at roughly the same time).
The questions remained unanswered for over seventy years. Between 1679 and 1680 Robert Hooke exchanged a series of letters with Isaac Newton. The letters covered a wide variety of scientific topics. In one of the letters, Hooke mentioned a hypothesis that the Sun exerted an inverse square force. Supposedly the Sun pulls on the planets, and this force gets stronger the closer you are to the Sun. Hooke claimed the force caused the elliptical orbits of the planets.
Newton replied he never heard of such a hypothesis. He thought about the problem and soon produced a proof that an elliptical orbit can result from an inverse square force. Newton was a very secretive man and began to view Hooke as a rival. He felt that Hooke didn’t have the mathematical skills to produce a proof himself and apparently saw no need to tell anyone that he had produced such a proof, especially Hooke.
In the meantime, Edmond Halley, a young astronomer with a variety of interests, started examining historical records of comets. Comets have been seen for hundreds of years and previous astronomers had made many observations. In 1682, he observed a bright comet. Halley had collected his comet observations and observations of other astronomers. When Newton found out, he asked Halley for copies. But Halley didn’t do anything further with comets (at least not for a while).
A few years later Hooke told Halley about the inverse square hypothesis and claimed he had a proof (it is unlikely Hooke had a proof, but Halley couldn’t have known that). Halley viewed it as a challenge, but slowly realized he needed help and so he went to visit Newton.
After this initial meeting, Halley visited Newton frequently, over the course of these visits Newton showed Halley his proof as well as many other unpublished papers. Halley realized there was a gold mine of ideas that no one else knew about. Halley wanted to Newton to publish. Newton was reluctant, but Halley was persistent. With a lot of encouragement from Halley, eventually The Principia, Newton’s masterpiece was published.
While it covers a variety of topics, for our purposes the most relevant part of The Principia is the theory of gravity. Newton assumed there was a gravitational force between every pair of objects (an inverse square force as Hooke had suggested). This force caused the apple to fall and the planets to move around the Sun.
However knowing there is a force is not enough to make a prediction; Newton showed how to take the gravitational force, the equation F=ma and a newly invented mathematical technique called the Calculus to compute an orbit. His technique didn’t always produce a result. If you have a system of two objects (say a star with a single planet), it tells us the objects will orbit in an ellipse, a parabola or a hyperbola (depending on the exact conditions). It doesn’t give us a result if there are three or more objects. In other words we can’t use this approach to compute the orbits in our solar system since there is the Sun, six planets (Uranus, Neptune and Pluto hadn’t been discovered yet), ten moons (four for Jupiter and six for Saturn) and an unknown number of comets. Something more is needed.
Producing an exact solution for Newton’s equations with more than two objects became known as the three body problem. Newton didn’t know how to solve the three body problem, he realized it was difficult (in fact he claimed it was too difficult for humans to solve). From the time of Newton up to the present, many people have studied it; some progress was made and a few specialized solutions were discovered.
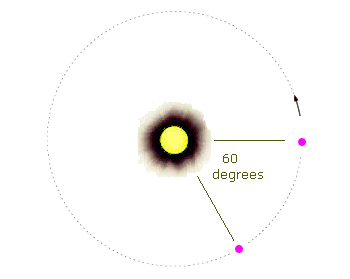
The easiest to explain involves a star and two planets. Assume that both planets are in the same elliptical orbit around the star. If the two planets are separated by 60 degrees, the planets will remain in the same orbit following Kepler’s equations separated by 60 degrees.
A few other solutions have been discovered. (I will not go into them here as they are harder to explain). However they are all special cases: of the numerous possibilities in the real universe, only a handful have an exact solution. It is unlikely that there ever will be an exact solution that applies to the real universe. This seems to imply we cannot compute the motion of anything.
But it isn’t hopeless; there are four general approaches. I’ll start with the first of these approaches (in future articles I will discuss the other three). Start with an exact solution (usually a two body solution but sometimes a three body solution). Then ask: what happens when additional bodies are added? We can’t get an exact solution, but we can approximate it by pretending the additional bodies “perturb” the motion of the other bodies. While I won’t go into the details, it is possible to calculate approximate orbits in this way (these approximate orbits are frequently very close to the correct result, so close the difference is often too small to be measured).
Different procedures are used for the three common cases: the planets, the moon, and comets. The procedures are similar; the biggest differences are caused by two facts: comets have more eccentric orbits than planets, and comets sometimes get close to the sun or a planet (usually Jupiter). The eccentric orbits and the close approaches make computations more complicated.
Newton made the first attempt to calculate the orbit of a comet. Halley used Newton’s technique and the observations of a comet to compute its orbital elements (a set of six numbers). Once the orbital elements are known, it was possible to obtain a Kepler orbit. (Getting good orbital elements can be tricky, inaccurate orbital elements will lead to inaccurate orbits). Halley repeated this for a number of comets and by 1705 he had determined that the comets of 1531, 1607, and 1682 had very similar orbits (as I mentioned above, Halley saw the comet of 1682). He concluded they were different apparitions of the same comet that took 76 years to orbit the sun (we now call it Halley’s comet). This proved at least one comet had an elliptical orbit. In time the orbits of other comets were computed. We now know that most comets travel in ellipses, but a few travel in parabolas or hyperbolas.
Jupiter and the other planets will perturb the Kepler orbit for a comet. Perturbations slowly shift orbital elements over time. Halley was the first to notice that Jupiter perturbed a comet. There is no known way to precisely calculate the effect, but over the next hundred years techniques to approximate perturbations were invented and slowly improved. These techniques were applied to both comets and planets. The fact that comets underwent perturbations was clear, but irregularities in the orbits of Jupiter and Saturn were noticed as well. These irregularities were accounted for by perturbations between these two planets as well as a new planet, Uranus. Using perturbation analysis and another technique (variation of the arbitrary constants), by 1800 astronomers were able to account for most of the irregularities of comet/planet/moon orbits. Even if you knew the orbital elements for a comet or planet, the orbital elements will need to be updated if you track the object over several months or longer. (There is no known way to calculate accurate orbits over extremely long periods, say a billion years or longer).
However there still were some issues. Tiny discrepancies in the orbit of the Moon couldn’t be accounted for. Starting with Newton and continuing up to this point, all calculations assumed that planets and other bodies were perfect spheres. Once astronomers realized that this oversimplification was the problem, the Moon’s orbit made sense (in brief—interactions between the Moon and the Earth’s oceans affect the Moon’s orbit). There also were tiny discrepancies in the orbit of Uranus and of Mercury that weren’t understood. These issues were also resolved eventually (with discovery of Neptune and General Relativity).
In part 3 of this article, I plan to give other examples on how Newton’s Law of Gravity is used.
The following references were used to prepare part 2.
Adams, Fred and Laughlin, Greg. 1999. The Five Ages of the Universe: Inside the Physics of Eternity. New York: The Free Press (A Division of Simon & Schuster, Inc.). [A discussion of one theory of the distant future of the universe. On page 51 the authors discuss a possible interaction between the sun, moon, the earth and a red dwarf. This section of the book suggests one reason why orbital predictions over billions of years are not possible].
Diacu, Florin and Holmes, Philip. 1996. Celestial Encounters: The Origins of Chaos and Stability. Princeton, New Jersey: Princeton University Press. [Can you predict the orbits of the planets over billions of years?]
Ferris, Timothy. 2003. Coming of Age in the Milky Way. New York: Perennial, an imprint of Harpers Collins Publishers [historical information on Kepler, Galileo, Halley and Newton].
Hawking, Stephen. 2004. The Illustrated on the Shoulders of Giants: The Great Works of Physics and Astronomy. Philadelphia, Pennsylvania: Running Press Book Publishers [historical information on Kepler, Galileo and Newton].
Halley, Edmond. A Synopsis of the Astronomy of Comets. Translated from the original, printed at Oxford. London, 1705. Based on information from English Short Title Catalogue. Eighteenth Century Collections Online. Gale Group. (Gale Document Number CW107356038).
Meeus, Jean. 1998. Astronomical Algorithms, 2nd Edition. Richmond, Virginia: Willmann-Bell, Inc [computing planetary orbits].
Moulton, Forest Ray. 1970. An Introduction to Celestial Mechanics, 2nd Revised Edition. New York: Dover Publications, Inc [computing planetary orbits].
Newton, Issac. 1999. The Principia, Mathematical Principles of Natural Philosophy. Translated by I. Bernard Cohen and Anne Whitman, assisted by Julia Budenz. Preceded by “A Guide to Newton’s Principia” by I. Bernard Cohen. London, England: University of California Press. [This is a translation of the 3rd edition of Philosophiæ Naturalis Principia Mathematica (or if you prefer English, Mathematical Principles of Natural Philosophy) written by Sir Issac Newton, 1726. It can be referred to as simply The Principia and describes Newton’s Theory of Gravitation among other things. The Principia has a well deserved reputation as difficult to follow. Early translations used archaic terminology. This translation is somewhat easier to read. The first half of the book gives a history of Newton including his interactions with Hooke and Halley, and how the The Principia came into being].