
Finding good optical tests has always been a problem for those who make optics. There are those who say, “If you can measure it, you can make it.” The contrapositive is usually presumed, but is clearly not true. Galileo’s lens makers had no way of testing lenses as they made them, but a recent interferogram of the (now broken) objective of Galileo’s telescope showed that it was made to an accuracy of about a twentieth of a wave, without the benefit of testing equipment, a feat which would be the envy of Perkin-Elmer today. Galileo was able to possess such an instrument by buying a lot of objective lenses, and discarding all but one or two, which is also a method still in use today.
Most of us don’t have the resources of Galileo or the Federal Government, so we must look for ways to make our optics right the first time. That usually means being able to test them with verifiable methods. There are many tests of astronomical optics used in the world today. The oldest test, the star test, was pioneered by Galileo himself. The star test, in capable hands, is a very good test of optics, not only because it tests the optic against the object that it will be used to see, but also because it permits the manufacture of essentially perfect optics. Under good seeing conditions, the test is “diffraction limited,” which means it is limited only by the physical nature of light. The star test’s only significant drawback is that it restricts testing to clear, steady nights, usually using the completed tube and mount to track the star being tested. While Astronomers have to work at night, Opticians usually prefer an 8 to 5 schedule.
The next important advance was made in 1859 by the Frenchman, Leon Foucault. He called his test the Knife-edge test, and it proved to be so incredibly sensitive that it was still the best test available when the 200” Hale telescope was figured. The Hale mirror was also tested by a method called the Hartmann test, but both tests have since been superseded by interferometric testing. The interference of light was known to Newton, but testing over distances greater than a couple of feet or so had to wait for the invention of the laser.
The Foucault test is one of the most sensitive tests of optics available. It is cheap and easy to do, which accounts for its almost universal use among amateur telescope makers. It basically consists of a light source, usually a small light bulb or LED, stopped down to a diameter near the mirror’s diffraction limit by a pinhole, and a knife edge, which may be a razor blade, an opaque piece of paper, or even a credit card.
The light from the pinhole is directed onto the mirror, and the reflected image of the pinhole is actively “cut off” by the knife edge. The idea is that a perfectly spherical mirror will form an image of the pinhole at a single point. When the knife edge is positioned with its edge at this point, a little motion of the knife edge at right angles to the beam will either let all of the light pass the knife edge and proceed into the eye, or will block all of the light. The mirror will appear to go from a bright disk to a dark disk. However, if the mirror’s surface is not entirely spherical, but rather has some “zones” whose slopes differ from those of the surrounding mirror, then light from these zones will not be returned precisely to that point. It may pass beyond the knife’s edge when light from the rest of the mirror has been cut off, and its source zone will appear bright when the rest of the mirror is dark.
A parabola, which is of interest to astronomers, is not a sphere, but can still be tested by the Foucault test. The tester merely adds a micrometer to his setup, and then measures the positions where light from successively larger ring zones of the mirror are brought to focus. In other words, he finds the point where the light from the center area (which has generally the same curvature) focuses, then where the light from the next larger zone focuses, and so on, to the edge. These measured positions are then compared to the positions where a good parabola should focus the light. Sometimes zonal masks are used to better isolate the area on the mirror to be measured. All of this is a tedious process, but in the hands of a skilled worker, can produce excellent feedback to the mirror maker about the shape of the surface of the mirror.
The test works best if the pinhole source and the knife edge are very close to each other, since an axially symmetric mirror (like a sphere or parabola) will not produce a perfect reflected image away from its axis. This fact has caused many people to build “slitless testers.” Construction details of these devices can be found in the literature.
I made a slitless tester many years ago, and it made a tremendous improvement to what I could see on the mirror. Zones that were very faint or did not exist, when the light source and knife edge were an inch apart, suddenly became very obvious when tested using a slitless tester. A mirror buyer should be very suspicious of the quality of a commercial mirror if the manufacturer’s web site shows them using a Foucault tester with a separated source and slit. They may be able to judge overall correction, but shallow zones just will not be seen. You can easily verify this for yourself by retesting your mirror with the source and knife edge separated. As an example, the tester sold by University Optics has the problem of a widely separated pinhole and knife edge.
The Foucault test can be very sensitive in a qualitative sense, but it is much harder to get data from it in a quantitative sense. The main problem I have had with this test is, if I could see an error on the mirror, how could I really tell how big the error was? The slope-step-slope-step method of judging a mirror’s overall correction seems loaded with opportunities to make errors. Where, really, is the 95% zone, where the mirror’s radius of curvature is changing so quickly and critically? Are the shadow intensities on either side of the mirror, either at the pins or in the mask cutouts, of equal intensity? Am I sure? Bouncing off of a good, well characterized aluminized flat would help here, and would turn Foucault zonal measurements into null testing for parabolic mirrors, but if there are zones in the mirror, however faint, there remains the problem of judging their size. And a double bounce off the unaluminized mirror’s surface means that the light source needs to be pretty bright, but can’t be a laser, because it is not advantageous to use coherent light for Foucault testing. (I used a very bright Zirconium arc lamp for a while. It solved the brightness problem, but not the measurement problem). The Foucault test also will not easily show astigmatism, when and if it is present, unless you specifically test for it. Even then, it is not easily detected.
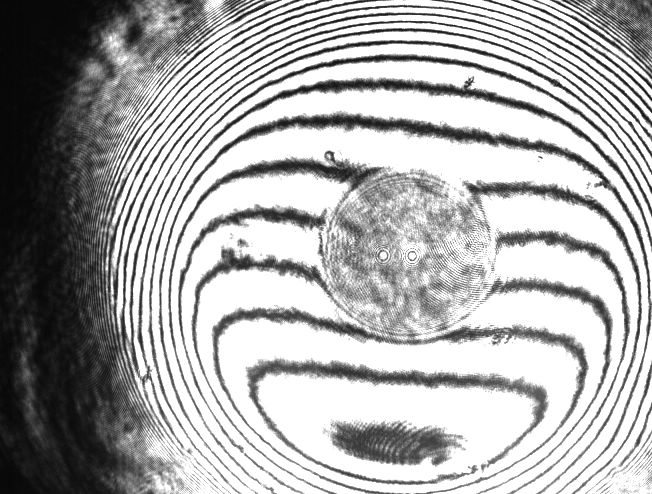
This, and other difficulties that I have had while testing mirrors by the Foucault method, caused me to move to a laser interferometer and Offner null optics. A laser interferometer shows deviations from perfection in half wave (or quarter wave, on double bounce) increments, with the option for estimating to an honest tenth or twentieth wave. When the Offner null lenses are added, accuracy is extended to testing conics other than parabolas. Laser interferometers have problems of their own, but they are all about the cost of entry, and not about the uncertainty of measured results.
There are some companies producing optics for amateurs today that say that interferometric testing is unnecessary, and they can get better results by using Ronchi, Foucault, and star tests. Their argument seems to be that interferometric testing is difficult to do properly, and interpreting the results is beyond the scope of the average buyer. I disagree with this, both for the reasons stated above, and because I have always considered the Ronchi test to be merely an out-of-focus Foucault test. Star testing, of course, is a perfectly valid and sensitive test, but is not practical for shop testing and is not capable of providing fast and, more importantly, detailed feedback when figuring the mirror.
In a future article, we’ll look at some of the strengths and weaknesses of interferometric testing.

“Wow, man! I guess I shouldn’t have duct taped the edge of my mirror to that plywood cell.”