Chapter 6 Process Models
Process models focus on mechanisms. These kinds of models allow us to model “what if” scenarios, such as what would happen to the spread of covid-19 cases if a state imposes a shelter-in-place order. The models in the previous chapters don’t allow us do such “what if” analyses in any reasonable manner. The material in the earlier chapters, however, allow us to justify some of the assumptions we may need in process models. Sometimes process models can be estimated directly from data, sometimes data merely provide ways of justifying assumptions one needs to make. Sometimes there is an “analyst-in-the-loop” aspect to these models because they may not be able to be estimated from data directly, so require the analyst to systematically modify a particular aspect of the model (e.g., an unknown parameter) to see how varying that aspect would affect the model’s outcome in a type of sensitivity or robustness analysis.
For an example of how we can use basic data along with some assumptions to estimate the “actual number of cases” check out this video.
A readable tutorial on process models in understanding pandemics is the book Charting the Next Pandemic by Pastore y Piontti et al. It was published prior to the current covid-19 pandemic. A more advanced treatment of some of these models using the statistical programming language R can be found in the book by Bjørnstad, Epidemics: Models and Data Using R, which is also available as a pdf through the UM library, along with the companion R package epimdr.
6.1 SIR Models
SIR models refer to a modeling approach that uses differential equations, which are equations that govern processes changes over time. The basic SIR model starts by having three kinds of people: Susceptible, Infectious and Recovered (SIR). In various versions of these models one could change assumptions such as “once an individual recovers they will not get the disease again because they develop antibodies” to “an individual who recovers has a p chance of being reinfected if they come in contact with an infected person” (where p is a probability between 0 and 1 and could be varied to study the implications). The wiki page on such models is not bad and provides a solid introduction; for a classic textbook on these models see Keeling and Rohani (2008).
Here is a 20min video on SIR models geared for the pandemic with examples around social distancing and a Washington Post article using an SIR approach to illustrate the effects of social distancing. The latter page appears below in a small interactive window (the cool web page within a web page trick—html only).
There are several R packages for SIR modeling, including EpiModel, EpiDynamics, and tsiR.
Some UM researchers have started analyzing the covid-19 pandemic using SIR models, these include
More generally, a UM team of Aaron King, Dao Nguyen and Ed Ionides have a general R package called pomp that can be used for simulation and estimation of SIR models, among other things.
Here I present a simple description of a basic and standard SIR model. Consider a population of size N that has S susceptible people, I infectious people and R recovered people such that the entire population size N must follow this restriction: N=S+I+R.
The model consists of three structural models, one for each of the changes in S, I and R. These equations, which look a lot like regression structural models with predictors such as \(\frac{IS}{N}\) multiplied by a \(\beta\), are
\[ \begin{aligned} \mbox{change S} &= \beta_1 \frac{ I S}{N}\\ \mbox{change I} &= \beta_1 \frac{ I S}{N} - \beta_2 I \\ \mbox{change R} &= \beta_2 I \end{aligned} \]
I’m abusing notation here because “change S” refers to the differential \(\frac{dS}{dt}\), which means the change in S for a small change in time. Without getting into the details of differential equations, for our purposes we can think of these like regression equations (the right hand side) modeling how much each of S, I and R change per unit time (the left hand side), but we have a system of three regression models that are further constrained by N=S+I+R. There are other details such as initial conditions that I won’t go into here. The underlying assumptions leads to some identification issues with parameters. For example, the \(\beta_1\) paramter is equal to the product between the number of average contacts a person has in unit time (\(\kappa\)) and a function of the probability of successful disease transmission (\(p\)); i.e., \(\beta_1 = \kappa * \log{(1-p)}\). Without additional data or assumptions, we merely work with \(\beta_1\) rather than its two components because we can’t tease them apart otherwise. It is like saying "5 = x*y, solve for x and y"—there are an infinite number of choices for x and y such that their product equals 5. In the case of SIR models, our data typically can estimate 5 but not the two separate components x and y.
The ratio of the two \(\beta\)s provides an interesting number. It is called the basic reproduction number and it is used so frequently that the ratio is given its own symbol \(R_0\) = \(\frac{\beta_1}{\beta_2}\). Intuitively, if we have a system where \(R_0\), say, equals 3, that means that on average 3 people get infected for every one person who is infected. Given the enrollment in this class of 70, my \(R_0\) as the instructor is 70 because I infected 70 people this year with my views on regression and multivariate statistics. The \(R_0\) establishes a criterion for whether an epidemic occurs, based on whether it is greater than or less than the proportion of susceptible people in the population at the start.
\(R_0\) provides ways of modeling various interventions such as the role of vaccinations in controlling an epidemic (see Bjørnstad’s book referenced earlier in this chapter). Under several assumptions, one can show that for diseases like measles (which has an \(R_0\) between 12 and 18 or as high as 20), it would require about 95% of the population to be vaccinated in order to contain the spread. The approximate expression to estimate the percentage of the population that would need to be vaccinated is p(vaccinated) = 1 - \(\frac{1}{R_0}\). If covid-19 has an \(R_0\)=2, then 50% of the population would need to be vaccinated, which means over 160 million people in the US would need to be vaccinated.
The value of \(R_0\) is not easy to estimate outside the model, though several methods have been proposed (see Bjørnstad’s book referenced earlier in this chapter). I won’t go into them here because they are all not on strong footing. For example, one approach requires using the regression on the log transform of the cumulative counts (what I presented in Chapter 5). But, we saw there that this log linear model had some systematic violations of the assumptions. Using parameters from suspect models to plug into other formulas leads to answers that are also suspect. Current estimates we are hearing from the US government is that \(R_0\) for covid-19 is between 2-3 prior to social distancing interventions but it isn’t clear how those estimates have been made. By comparison, the usual influenza has an \(R_0\) of about 1.3.
This particular SIR model makes predictions about the underlying process that can be tested and that also lead to ideas for how to intervene in a pandemic. For example, the model shows that it is sometimes easier to control a pandemic by decreasing the number of infected individuals, say, through social distancing, rather than decreasing the number of susceptible people, say, through vaccination. Of course, that may not be the case in reality, but these are the kinds of testable implications a model can give and the kinds of ideas for interventions that grow out of such models (i.e., under this particular SIR the key intervention is to reduce the number of infected individuals, say, through interventions such as social distancing and stay-at-home orders).
There is much that has been written about SIR models and there are many variants. These include the population size increasing/decreasing due to births, migration, and deaths, which end up affecting the overall dynamics of S, I and R proportions (e.g., are there new “susceptible” people recruited into the system? or are people “leaving” the system, say, due to death?). The model can also be extended to include characteristics of individuals, such as age, which can be useful in modeling some diseases that impact groups of individuals differentially.
A simple interactive demo in R is provided by the shinySIR package (see vignette for instructions). I print the command line here but it needs to be run locally on your computer with R installed because the program opens a browser that allows you to interact.
We aren’t in a position to use SIR in a more data-driven way because we don’t have complete numbers. For example, the recovered numbers are no longer reported in the US because the data are suspect (e.g., the Johns Hopkins repository). Without complete data it makes it difficult to work with estimating SIR models. Though see efforts by Peter Song and colleagues to model data from China. As we saw in Chapter 5, even with incomplete data, if one is willing to make assumptions, it is possible to use the model to help us understand some of the underlying mechanisms involved in disease transmission and explore the impact of potential interventions.
6.1.1 Exponential and Logistic Growth Models
In the previous chapter I fitted both exponential and logistic growth models. It is useful to consider the change processes that these two simple models imply. We can use differential equations machinery, as is done for SIR models, to understand these two types of growth models. In the first case, if change is related to the current value times a constant (much like a savings account that has today’s change in balance equal to the principal times the interest rate):
\[ \begin{aligned} \mbox{change C} &= \beta_1 f(t)\\ \end{aligned} \] where the “change C” refers to the differential \(\frac{dC}{dt}\), which means the change in the count C for a small change in time. The solution to this change equation has the form \(\beta_2 e^{\beta_1 t}\), meaning this is the most general function that produces that type of change. Note that the SIR model has three such change equations, similar in form to this one, so the SIR model has an exponential growth aspect but there is also the given-and-take between the three compartments (the number of people in each of the three categories S, I and R) that provides additional constraints on the nature of the exponential growth that an SIR-based model exhibits.
A different type of change follows this equation
\[ \begin{aligned} \mbox{change C} &= \beta_1 f(t)*(1-f(t)) \end{aligned} \] Let’s consider the case where f(t) is constrained to be between 0 and 1, so behaves like a proportion (e.g., the proportion of the population that is in the suspectible compartment). Under this condition, change is maximal when f(t)=.5 and change magnitude decreases as f(t) moves away from .5. We can ask a similar question as before, what is the most general function f that satisfies this change equation? It turns out that f(t) is the logistic growth equation of the form \(\frac{1}{1+\beta_2 e^{-\beta_1 t}}\) where \(\beta_2\) is the integration constant, which is similar to the form I used in the previous chapter (it included an asymptote as an estimate rather than fixed to a constant and did not have a multiplier to the \(\exp\) term). In principle, one could build SIR-like models that follow different change equations, and then the resulting model could exhibit different behavior. This is what makes building models a complex endeavor, but we can use the observations to help us figure out properties of the underlying mechanisms.
6.1.1.1 Phase Plots
It is useful to consider what is called a phase plot. There are several forms of this type of plot. The one I’ll use here has f(t) on the horizontal axis and f(t+1) on the vertical axis. Thus, unlike many of the plots we have considered so far in these notes that has time as an explicit variable on the horizontal axis, the phase plot has time as an implicit variable because the two axes are both observations of counts and time produces a trajectory in this plot as points move from time t to t+1.
Here is the characteristic plot of a standard change process following an exponential form. I’ll use our best fitting exponential function across the the 50 states that we computed in the previous chapter. The numbers in the plot refer to the day variable and each point is (count(t), count(t+1)) meaning the count for time t and the count for time t+1.
exp.pred.ts <- ts(diff(nydf.exponential$prediction))
plot(exp.pred.ts, stats::lag(exp.pred.ts, 1), cex = 0.5,
col = "blue", main = "Phase plot of New York Positive Counts for the Exponential Model",
xlab = "count(t)", ylab = "count(t+1)", xlim = c(0.009,
0.036), ylim = c(0.009, 0.036))
abline(0, 1)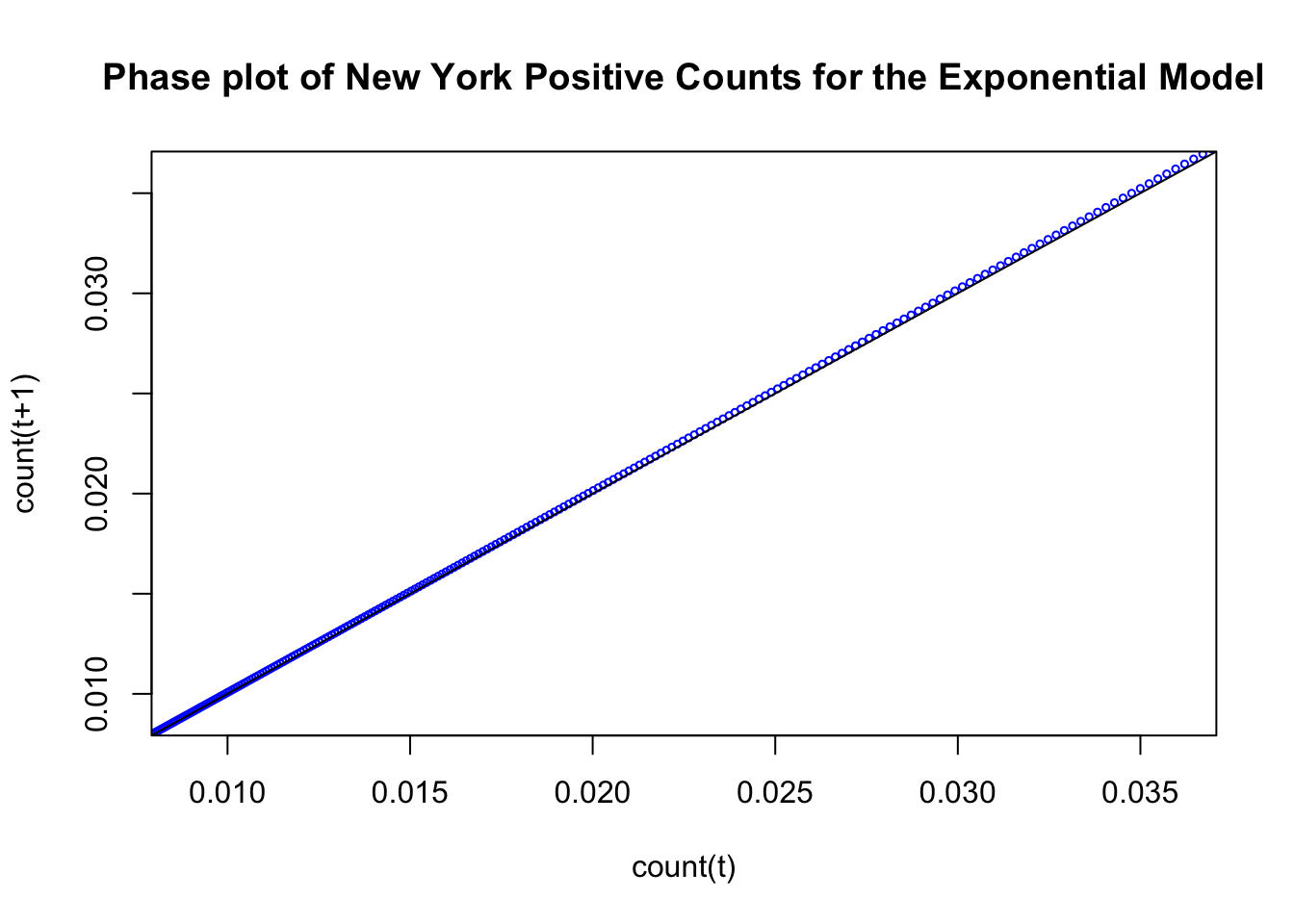
Sometimes this plot is produced in the form of a cobweb by including the step function movements of this trajectory. It looks like a step function because the current output count(t+1) becomes the next time’s input. So the trajectory moves to the left and up at each time step. Here is the same figure redrawn with the step function in red.
exp.pred.ts <- ts(diff(nydf.exponential$prediction))
plot(exp.pred.ts, stats::lag(exp.pred.ts, 1), cex = 0.5,
col = "blue", main = "Phase plot of New York Positive Counts for the Exponential Model",
xlab = "count(t)", ylab = "count(t+1)", xlim = c(0.009,
0.036), ylim = c(0.009, 0.036))
abline(0, 1)
lines(c(exp.pred.ts), c(stats::lag(exp.pred.ts, 1)), col = "red",
type = "S")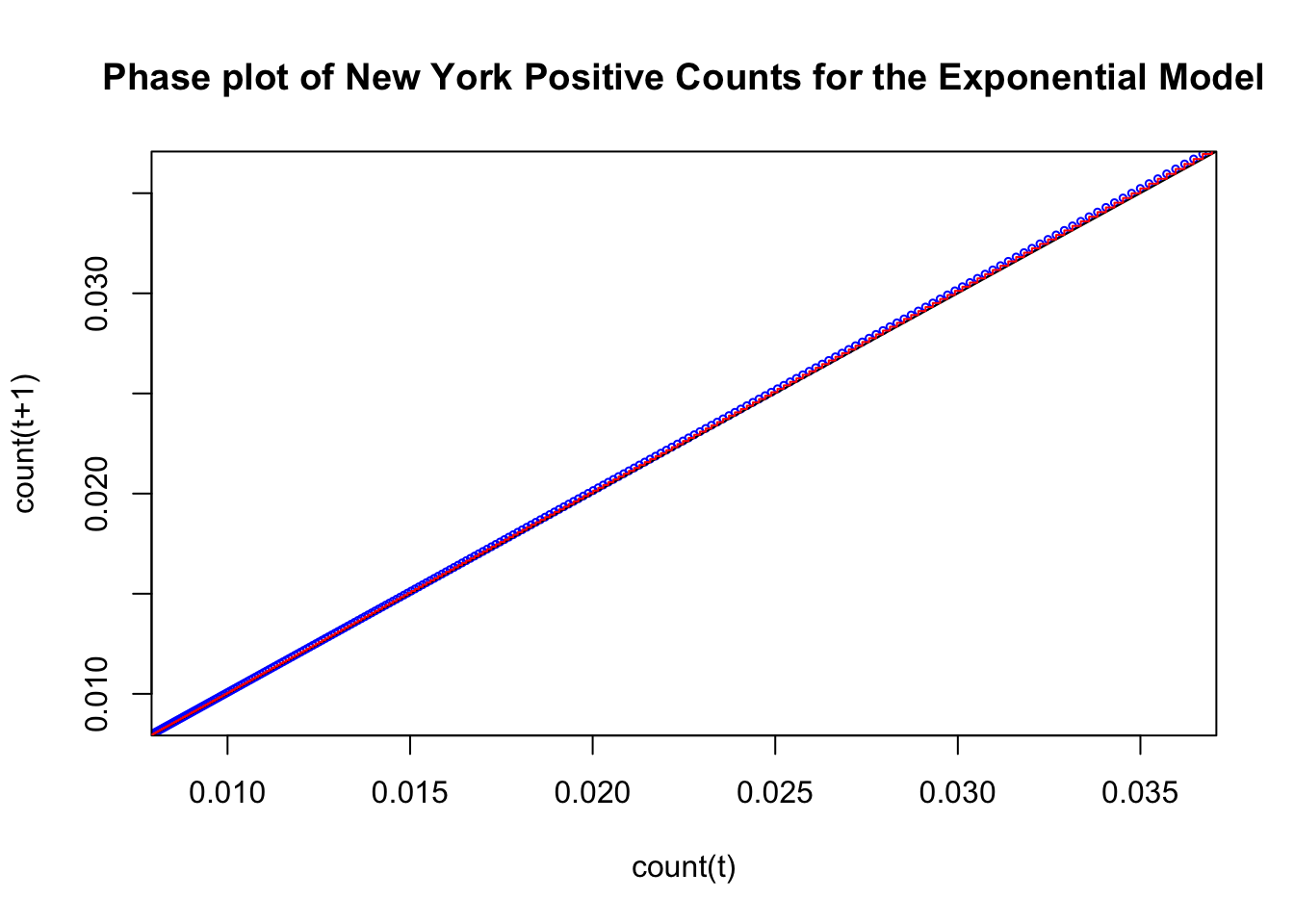 This plot illustrates the key property of exponential growth. Movement in phase space is away from the identity line (the magnitude of the changes increases in time) and the trajectory as time ticks away is movement in the plot from left to right. This is analogous to your savings account balance increasing at each time step with compound interest. This best fitting exponential model to the 50 states follows a phase plot that behaves like an exponential model. One needs to realize that the actual data may not have a phase plot that behaves like this as we will see at the end of this subsection. In the current plot we are seeing the behavior of the exponential model with parameter estimates that are optimallly selected for this data set.
This plot illustrates the key property of exponential growth. Movement in phase space is away from the identity line (the magnitude of the changes increases in time) and the trajectory as time ticks away is movement in the plot from left to right. This is analogous to your savings account balance increasing at each time step with compound interest. This best fitting exponential model to the 50 states follows a phase plot that behaves like an exponential model. One needs to realize that the actual data may not have a phase plot that behaves like this as we will see at the end of this subsection. In the current plot we are seeing the behavior of the exponential model with parameter estimates that are optimallly selected for this data set.
We can also examine the analogous phase plot for the logistic growth model that we estimated on the 50 states in the previous chapter. Recall that for the logistic growth model we used actual the count rather than the percentage of the state population as we did for the exponential function, so I’ll maintain that here. This is a busy plot but take the two pieces separately. The blue trajectory numbered 1 to maximum t is the path the logistic growth model follows in this phase plot. Note that the blue trajectory lookis similar to an exponential growth model up to about the 22nd time step or so, and then begins to move closer to the identity line and eventually changes direction to the last set of time steps is moving back to starting point. This is the characteristic pattern of the logistic growth model. The red step function is there to remind us that the movement follows a step function because we have discrete time.
logistic.pred.ts <- ts(diff(nydf.logistic$prediction))
plot(logistic.pred.ts, stats::lag(logistic.pred.ts, 1),
cex = 0.5, col = "blue", main = "Phase plot of New York Positive Counts for the Logistic Model",
xlab = "count(t)", ylab = "count(t+1)")
abline(0, 1)
lines(c(logistic.pred.ts), c(stats::lag(logistic.pred.ts,
1)), col = "red", type = "S")
Now that we have a clear understanding of the phase plots the exponential and logistic growth models produce we can examine the phase plot of the actual data.
data <- data.frame(days = actualny$x[-1], counts = actualny$y[-1])
time.series.day.counts <- ts(diff(data$counts))
plot(time.series.day.counts, stats::lag(time.series.day.counts,
1), cex = 0.5, col = "blue", main = "Lag plot of New York Positive Counts",
xy.lines = F, xy.labels = T, xlab = "count(t)", ylab = "count(t+1)")
abline(0, 1)
lines(c(time.series.day.counts), c(stats::lag(time.series.day.counts,
1)), col = "red", type = "S")
While the count data for New York do not look like like the same phase plot we saw for the best fitting logistic growth model, this phase plots has some features associated with the logistic growth model such as initial general movement from left to right up to a particular time and then a general movement from right to left. There are other patterns present in the data phase plot that are not present in the phase plot of the best fitting logistic growth, such as the apparent “rectangular movements.” These “rectangular” movements are also consistent with the pattern of a basic logistic growth (see cobweb plot), which shows the “rectangular” patterns in the phase plots occur for particular values of \(\beta_1\). We can explore how the particular choice of logistic growth model I chose in the previous chapter may have been an inadequate representation of the data even though the algorithm was able to estimate the best fitting parameters.
The “rectangular patterns” that occur happen to coincide with the part of the incidence plots where we saw a bit of noise. For example, in the machine learning section of the previous chapter, we saw a section of the data from New York where the change was relatively flat but the variability in that region happened to be more pronounced. It is possible that this behavior could be due to basic logistic growth The logistic form I used in the nonlinear estimation routine was not able to capture this pattern so the “rectangular” pattern gets relegated to the residual. In other words, there is the part that corresponds to the “Y hat” of a regression approach (what the model predicts) and the part that corresponds to the additive error term (the “plus \(\epsilon\)” part of the model). The estimation algorithm may move particular parts of the ‘data pattern’ to the “Y hat” portion and other parts to the "plus \(\epsilon\) part. If when examining the residuals we still see a pattern in them and if we follow standard practice in nonlinear estimation, we would go down the route of exploring different structure on the residuals (such as ARMA models or allowing for heterogeneity of error variance) rather than questioning the very form of the logistic regression equation we used in the nonlinear regression. Modeling choices have implications for how various parts of signal in data are parsed and handled.
This shows the importance of examining one’s data in different ways. The phase plot uses the same information as the cumulative plot and the incidence plot that we have examined extensively throughout these notes. Even though we are examining the same counts of positive tests here, quite a different insight emerges from this plot than from the other plots. This subsection also highlights the importance of examining one’s modeling decisions. Do we go with a simple form of logistic growth? Do we go with a more complex form (as was done in the previous chapter with additional parameters such as the asymptote) and tease apart the pattern of that model from the pattern in the residuals? Some additional questions involve how we should incorporate measurement error and noise into this modeling. Is the simple and standard “plus \(\epsilon\)” approach to noise adequate in this setting or should we consider a different approach where noise is built into the system directly?
6.1.2 SIR summary
This gives you a flavor of how to go about building this kind of process model. Work with models of how a system and its variables change over time involves figuring out those change properties and deriving the underlying functions that give rise to those change equations. This style of modeling places emphasis on the underlying process, and data are used to estimate parameters and adjudicate between different possible change models, rather than using the models to play a curve fitting game. There are many extensions of SIR models that have additional “compartments” like Death or Exposed or Birth, so in addition to S, I and R some people die so they are out of the system and that changes the number N, which places constraints on S, I and R, or new individuals enter the system say through birth, which also affects N and hence the number of individuals who are susceptible.
6.2 Network-based SIR Models
A different version of SIR models focuses along movements in a network. These types of models are not based on differential equations as those we saw in the previous section.
In lecture I’ll play with this interactive demo Twitch-style (game streaming).
Here is a link to a more sophisticated network SIR model.
6.3 Agent-based Models
In class I’ll play with a Netlogo demo on virus spread. This represents a different type of model that endows individual agents with particular properties, sets up the rules for how these agents “interact” and then simulates repeated interactions among these agents. These are powerful modeling approaches. A relatively simple way to program these models is through the logo language, originally developed to teach children how to program (e.g., moving a turtle around a space and the turtle follows particular rules when interacting with the environment).
Network-based models (previous subsection) and agent-based models share similarities with more equation-based SIR models in that they work on observed variables and try to model behaviors at multiple levels of analysis in hopes of understanding the underlying dynamics of the system. There are also differences between these approaches. For example, equation-based models tend to tackle the system more directly (e.g., in the SIR models the equations involve interconnected variables, seen, for instance, in how the three standard SIR equations involve terms from the other equations) whereas agent-based and network models tend to focus just on the behavior of individuals and possibly their immediate neighbors without much information about processes operating at other levels. For more on these distinctions see a paper by Van Dyke Parunak, Savit and Riolo.
One could work with netlogo directly but it is probably better to use a workflow that includes R so you can make use of data and other R resources such as graphics. There is an R package nlrx that creates an R interface to netlogo. It requires some work in setting things up, which vary depending on whether you have a mac or a pc. There is another package RNetLogo that provides a different interface but it doesn’t look like it has been updated since 2017 so use with caution. There is also a way to call R commands within netlogo.
These are all fussy though as they require a clean java installation and I’ve been having problems with rJava on my mac for several months, even with new installations. Still waiting for a fix.
Here is a video of a screen capture while I interacted with netlogo. I used the example Virus model that is an agent-based SIR-style model. Sick (red) agents infect other agents when they bump into each other, green agents are healthy and gray agents are immune/recovered. The video starts with the infectiousness rate set relatively low and after a few time steps the sick agents drop out. Then I change I increase the infectiousness parameter and we see a cyclic pattern where the number of sick increases and decreases but the number of sick agents doesn’t seem to go to zero. One plays with the parameters to get intuition of how this system behaves. This can be extended in a variety of ways such as endowing the agents with different behaviors.
6.4 Public Policy Models
A major aspect of public policy models involves scenario planning to facilitate decision making in a manner that considers objectives as well as minimizing unintended consequences. This can be done using qualitative or quantitative methods. Here is a link to one example of a quantitative approach using simulation methods. You can search for a specific hospital in their data base or enter assumptions, sliders allow you to vary attributes such as the effectiveness of social distancing policies, the percentage of elective surgeries that are cancelled,, number of ventilators available, etc., in order to model the available capacity of various resources such as available hospital beds, available ventilators, and numer of PPE equipped nursing staff. Think a game like SimCity.
Another scenario planning tool is through Rush University with the interactive calculator I described in Chapter 5. Below the modeling of positive test cases section the user has the ability to vary assumptions such as the percentage admitted to critical care and the lag time in days between onset of symptoms and the hospital visit to forecast number of beds needed (both critical and non-critical care) and the number of PPE supplies needed.
While the interactive tools are useful to gain an intuitive understanding of the role each factor plays, a more systematic approach is used where a program cycles through many levels of each of the factors, examining all the possible combinations (possibly weighting them by their probabilities and uncertainty), to arrive at a distribution of possible outcomes. These models are useful to run several “what-if” scenarios and understand the overall picture. There is a balance one needs to strike between making this modeling simple, tractable and interpretable versus growing the number of variables to enhance realism. The best case is if the model is mature and has been evaluated against other data, such as historical data, to see how well it does. In the middle of a pandemic we don’t have the luxury of performing years of research to evaluate different modeling approaches. An example of this type of modeling is being conducted by a group based at Northeastern University using the GLEAM model (see fig 2).
6.5 Summary
The process models I’ve reviewed in this chapter have a strong public health and epidemiological perspective. Most don’t work with data directly but take as input parameters that may be based on data you collect (e.g., determining the contagious period of a virus). They are not like the usual statistical models such as regression where data are used to estimate the model parameters using goodness of fit measures and “optimal” parameters are computed. Instead, these models are more like “analyst-in-the-loop” because they require the analyst to make assumptions, run the simulation, perform gut checks on the results, and tinker with the assumptions to improve the model. At minimum, these process models can provide insight into the underlying mechanisms.