Chapter 8: Multiple Reactions

Gas Phase Multiple Reactions in a Membrane Reactor with Pressure Drop

Case 1 Large sweep gas velocities CCsg = 0

Open the Polymath file for Case 1 by clicking here

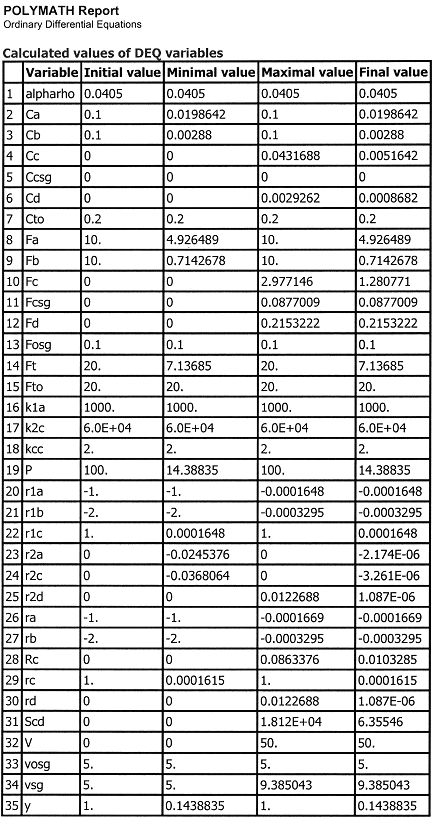
POLYMATH report table displaying calculated values of differential equation (DEQ) variables. Columns include initial, minimal, maximal, and final values for variables such as alpharho, Ca, Cb, Cc, Cd, Cto, Fa, Fb, Fc, Fd, Ft, k1a, k2c, kcc, P, reaction rates (r1a, r1b, r1c, r2a, r2c, r2d, ra, rb, rc, rd), Scd, V, vosg, vsg, and y.

List of differential equations: 1) d(Fa)/d(V) = ra, 2) d(Fb)/d(V) = rb, 3) d(Fc)/d(V) = rc - Rc, 4) d(Fd)/d(V) = rd, 5) d(Fcsg)/d(V) = Rc * Cc, 6) d(y)/d(V) = -alpharho / 2 / y * (Ft / Fto).

List of explicit equations: 1) Fosg = 0.1, 2) vosg = 5, 3) vsg = vosg * (Fosg + Fcsg) / Fosg, 4) P = y * 100, 5) Ccsg = Fcsg / vsg * 0, 6) Ft = Fa + Fb + Fc + Fd, 7) k1a = 1000, 8) k2c = 60000, 9) Cto = 0.2, 10) Ca = Cto * (Fa / Ft) * y, 11) Cb = Cto * (Fb / Ft) * y, 12) Cc = Cto * (Fc / Ft) * y, 13) r1a = -k1a * Ca * Cb^2, 14) r1b = 2 * r1a, 15) rb = r1b, 16) r2c = -k2c * Ca^2 * Cc^3, 17) r2a = 2/3 * r2c, 18) r2d = -1/3 * r2c, 19) r1c = -r1a, 20) rd = r2d, 21) ra = r1a + r2a, 22) rc = r1c + r2c, 23) Fto = 20, 24) alpharho = 0.0405, 25) kcc = 2, 26) Rc = kcc * (Cc - Ccsg), 27) Cd = Cto * (Fd / Ft) * y, 28) Scd = if(V > 0.0001) then ((Fc + Fcsg) / Fd) else (0).

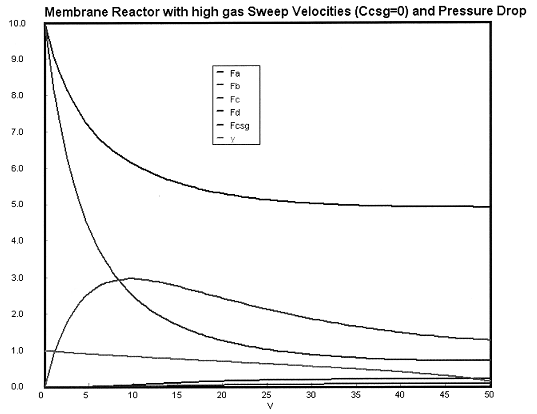
Graph showing a membrane reactor with high gas sweep velocities (Ccsg = 0) and pressure drop. The x-axis represents reactor volume (V), and the y-axis represents molar flow rates for components Fa, Fb, Fc, Fd, Fcsg, and y. Fa decreases sharply, Fb peaks and declines, while Fc and Fd increase gradually.

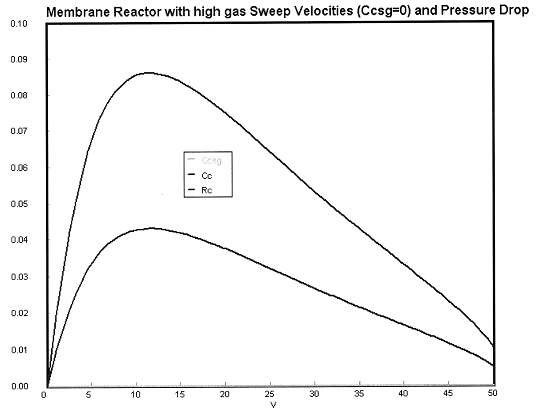
Graph showing the profiles of Cc and Rc in a membrane reactor with high gas sweep velocities (Ccsg = 0) and pressure drop. The x-axis represents reactor volume (V), and the y-axis represents the values of Cc and Rc. Both Cc and Rc increase, peak, and then gradually decrease as the volume increases.

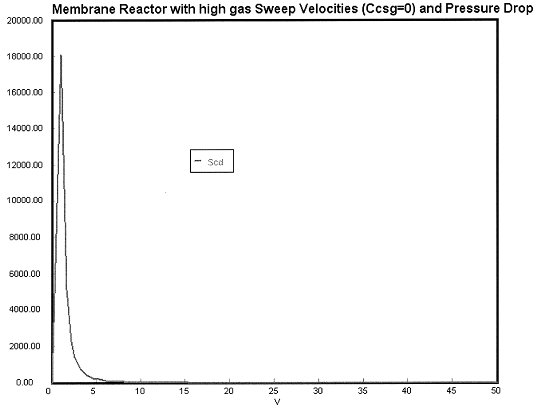
Graph showing the profile of Scd in a membrane reactor with high gas sweep velocities (Ccsg = 0) and pressure drop. The x-axis represents reactor volume (V), and the y-axis represents the value of Scd, which decreases sharply and stabilizes as the volume increases.

Case 2A Moderate to Low Sweep Gas Velocity CCsg = FCsg/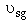

Open the Polymath file for Case 2 by clicking here

Entering sweep gas molar flow rate: \(F_{osg} = 0.1 \, \text{mol}/\text{min}\)

Entering sweep gas volumetric flow rate: \(\nu_{osg} = 5 \, \text{dm}^3/\text{min}, \, \nu_{sg} = 5 \left(\frac{0.1 + F_{csg}}{0.1}\right)\)

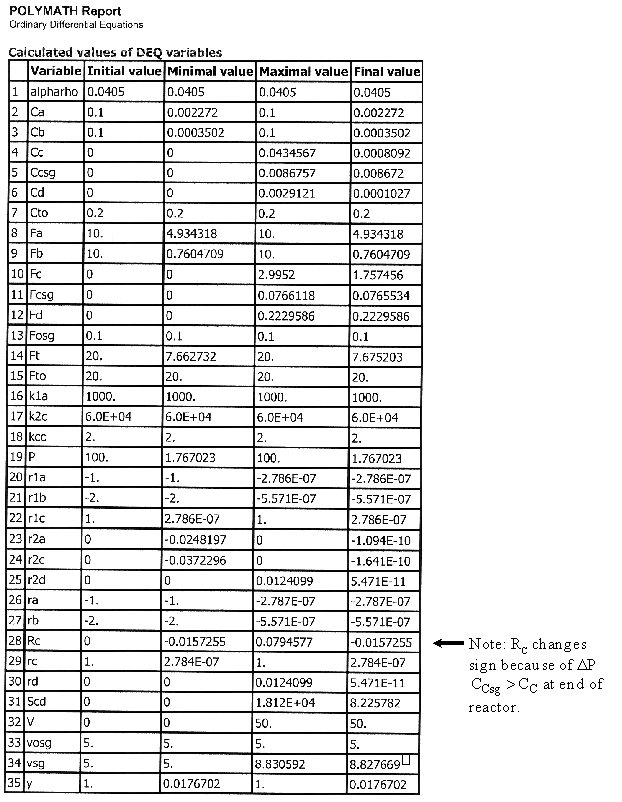
POLYMATH report table showing calculated values of differential equation (DEQ) variables, including initial, minimal, maximal, and final values for variables like alpharho, Ca, Cb, Cc, Ccsg, Cd, Cto, Fa, Fb, Fc, Fcs, Rd, Ft, k1a, k2c, kcc, P, reaction rates (r1a, r1b, r1c, r2a, r2c, r2d, ra, rb, Rc, rc, rd), Scd, V, vosg, vsg, and y. A note indicates Rc changes sign due to ΔP where Ccsg > Cc at the end of the reactor.

List of differential equations: 1) d(Fa)/d(V) = ra, 2) d(Fb)/d(V) = rb, 3) d(Fc)/d(V) = rc - Rc, 4) d(Fd)/d(V) = rd, 5) d(Fcsg)/d(V) = Rc * Cc, 6) d(y)/d(V) = -alpharho / 2 / y * (Ft / Fto).

List of explicit equations: 1) Fosg = 0.1, 2) vosg = 5, 3) vsg = vosg * (Fosg + Fcsg) / Fosg, 4) P = y * 100, 5) Ccsg = Fcsg / vsg, 6) Ft = Fa + Fb + Fc + Fd, 7) k1a = 1000, 8) k2c = 60000, 9) Cto = 0.2, 10) Ca = Cto * (Fa / Ft) * y, 11) Cb = Cto * (Fb / Ft) * y, 12) Cc = Cto * (Fc / Ft) * y, 13) r1a = -k1a * Ca * Cb^2, 14) r1b = 2 * r1a, 15) rb = r1b, 16) r2c = -k2c * Ca^2 * Cc^3, 17) r2a = 2/3 * r2c, 18) r2d = -1/3 * r2c, 19) r1c = -r1a, 20) rd = r2d, 21) ra = r1a + r2a, 22) rc = r1c + r2c, 23) Fto = 20, 24) alpharho = 0.0405, 25) kcc = 2, 26) Rc = kcc * (Cc - Ccsg), 27) Cd = Cto * (Fd / Ft) * y, 28) Scd = if(V > 0.0001) then ((Fc + Fcsg) / Fd) else (0).

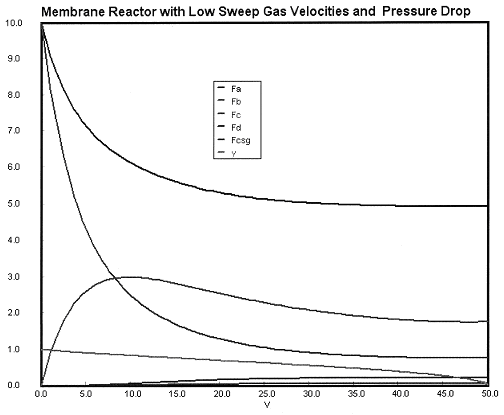
Graph showing a membrane reactor with low sweep gas velocities and pressure drop. The x-axis represents reactor volume (V), and the y-axis represents molar flow rates for components Fa, Fb, Fc, Fd, Fcsg, and y. Fa decreases sharply, Fb peaks and declines, while Fc and Fd increase gradually, with Fcsg and y remaining relatively steady.

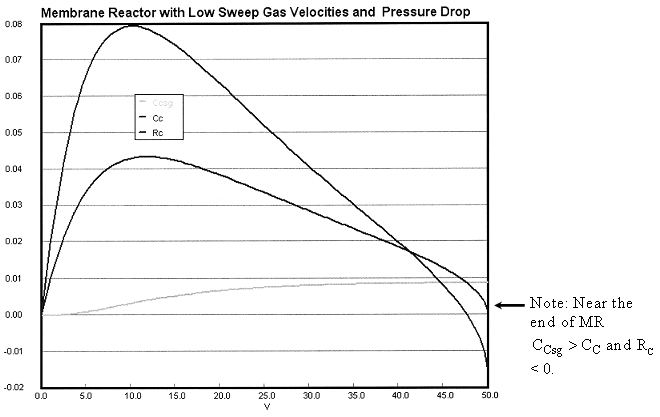
Graph showing the profiles of Cc and Rc in a membrane reactor with low sweep gas velocities and pressure drop. The x-axis represents reactor volume (V), and the y-axis represents the values of Cc and Rc. Both Cc and Rc increase, peak, and then decline. A note indicates that near the end of the membrane reactor (MR), Ccsg > Cc and Rc < 0.

Case 2B Low Sweep Gas Velocity and No Pressure Drop

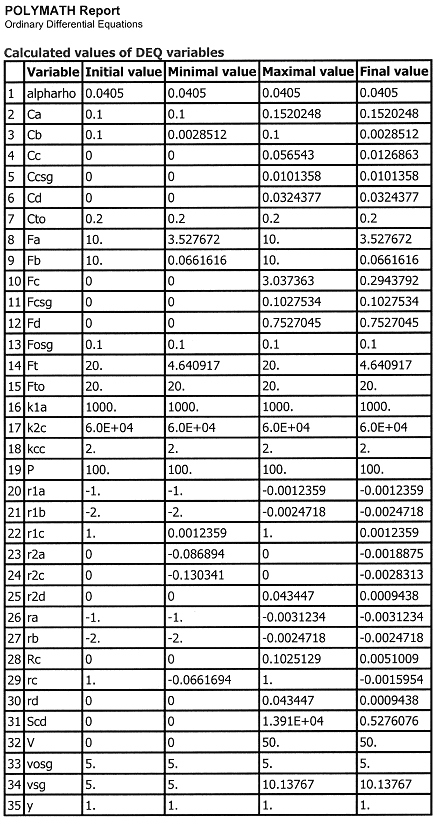
POLYMATH report table displaying calculated values of differential equation (DEQ) variables, including initial, minimal, maximal, and final values for variables like alpharho, Ca, Cb, Cc, Ccsg, Cd, Cto, Fa, Fb, Fc, Fcsg, Fd, Fosg, Ft, Fto, k1a, k2c, kcc, P, reaction rates (r1a, r1b, r1c, r2a, r2c, r2d, ra, rb, Rc, rc, rd), Scd, V, vosg, vsg, and y.

List of differential equations: 1) d(Fa)/d(V) = ra, 2) d(Fb)/d(V) = rb, 3) d(Fc)/d(V) = rc - Rc, 4) d(Fd)/d(V) = rd, 5) d(Fcsg)/d(V) = Rc * Cc, 6) d(y)/d(V) = -alpharho / 2 / y * (Ft / Fto) * 0.

List of explicit equations: 1) Fosg = 0.1, 2) vosg = 5, 3) vsg = vosg * (Fosg + Fcsg) / Fosg, 4) P = y * 100, 5) Ccsg = Fcsg / vsg, 6) Ft = Fa + Fb + Fc + Fd, 7) k1a = 1000, 8) k2c = 60000, 9) Cto = 0.2, 10) Ca = Cto * (Fa / Ft) * y, 11) Cb = Cto * (Fb / Ft) * y, 12) Cc = Cto * (Fc / Ft) * y, 13) r1a = -k1a * Ca * Cb^2, 14) r1b = 2 * r1a, 15) rb = r1b, 16) r2c = -k2c * Ca^2 * Cc^3, 17) r2a = 2/3 * r2c, 18) r2d = -1/3 * r2c, 19) r1c = -r1a, 20) rd = r2d, 21) ra = r1a + r2a, 22) rc = r1c + r2c, 23) Fto = 20, 24) alpharho = 0.0405, 25) kcc = 2, 26) Rc = kcc * (Cc - Ccsg), 27) Cd = Cto * (Fd / Ft) * y, 28) Scd = if(V > 0.0001) then ((Fc + Fcsg) / Fd) else (0).

We see that when there is no pressure drop CC is always grater than CCsg and species C does not diffuse back into the reactor.




Back to Chapter 8