Chapter 5: Isothermal Reactor Design: Conversion
What Four Things are Wrong with this Solution?
Problem
The elementary gas phase reaction A + 2B --> C is carried out in a packed bed reactor. Calculate the exit conversion from a PBR packed with 800 kg of catalyst. The feed is stoichiometric.
Additional Information
\(\alpha = 0.001 \, \text{kg}^{-1}\)
\(C_A = 0.04 \, \text{mol}/\text{dm}^3\)
\(k = 3.0 \, \text{dm}^6/\text{mol}^2 \cdot \text{s}\)
\(v_0 = 20 \, \text{dm}^3/\text{s}\)
Solution
Equations:
\(\frac{d(X)}{d(W)} = \frac{-\text{raprime}}{F_{A0}}\)
\(k = 3\)
\(C_{A0} = 0.04\)
\(\alpha = 0.001\)
\(v_0 = 20\)
\(y = (1 - \alpha W)^{0.5}\)
\(F_{A0} = C_{A0} \cdot v_0\)
\(C_A = C_{A0} (1 - X) y\)
\(C_B = C_{A0} (1 - X) y\)
\(\text{raprime} = -k \cdot C_A \cdot C_B\)
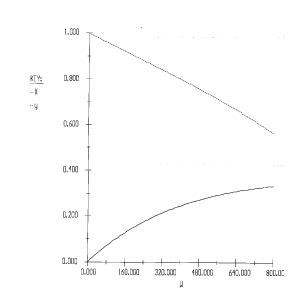
\(W_0 = 0, \, W_f = 800\)
Initial Value: 0
|
|
1) The rate law is incorrect. It should be: \(r_A = -kC_A C_B^2\)
2) The concentrations are incorrect, the feed is stoichiometric.
\(\text{Therefore: } \Theta_B = 2\)
3) The volume change was not included.
\(v = v_0 (1 + \varepsilon X) \frac{P_0}{P} \frac{T}{T_0} = v_0 (1 + \varepsilon X)\)
\(\varepsilon = -y_{A0} \delta = -\frac{1}{3}(1 - 1 - 2) = -\frac{2}{3}\)
\(C_A = C_{A0} \left[\frac{(1 - X)}{(1 - \frac{2}{3} X)}\right] = \frac{2 C_{A0} (1 - X)}{(1 - \frac{2}{3} X)} y\)
4) The equation for \(y\) is incorrect. There is volume change and \(y = (1 - \alpha W)^{1/2}\) can only be used when \(\varepsilon = 0\). Therefore, the form of the momentum balance that must be used is
\(\frac{dy}{dw} = -\frac{\alpha (1 + \varepsilon X)}{2y}\)
Corrected Solution
Equations:
\(\frac{d(y)}{d(W)} = -\frac{\alpha}{2} \cdot \frac{y}{(1 + \text{eps} \cdot X)}\)
\(\frac{d(X)}{d(W)} = -\frac{\text{raprime}}{F_{A0}}\)
\(\alpha = 0.001\)
\(\text{eps} = -\frac{2}{3}\)
\(k = 3\)
\(C_{A0} = 0.04\)
\(v_0 = 20\)
\(F_{A0} = C_{A0} \cdot v_0\)
\(C_A = C_{A0} \cdot (1 - X) \cdot y / (1 + \text{eps} \cdot X)\)
\(C_B = C_{A0} \cdot 2 \cdot (1 - X) \cdot y / (1 + \text{eps} \cdot X)\)
\(\text{raprime} = -k \cdot C_A \cdot C_B^2\)
\(W_0 = 0, \, W_f = 800\)
Initial Value:
1, 0