Chapter 5: Isothermal Reactor Design: Conversion

More

Suppose we have two samples, each with 8.38 grams of catalyst. One sample contains 10 spheres, each weighing 0.838 and one sample contains just one sphere of 8.38 g. Which sample has the greater external surface area for the molecules to enter the catalyst?

   Diagram of 10 small circles arranged in a grid-like pattern with the text '8.38 g' displayed below the diagram.       A single outlined circle with the text '8.38 g' displayed below the circle.   

\(\text{mass} = \rho_c V = \rho_c \frac{4\pi D_P^3}{3}\)

\(\rho_c = 2 \, \text{g}/\text{cm}^3\)

8.38 g 8.38g

Surface area = number of particles x surface area of one particle = n π DP2

Large Particles Small Particles

\(8.38 = \frac{(2)(4)\pi D_P^3}{3}\)

\(D_P^3 = 1 \, \text{cm}^3\)

\(D_P = 1 \, \text{cm}\)

\(\text{Surface area} = \pi D_P^2 = \pi (1)^2 = 3.14 \, \text{cm}^2\)

\(8.38 = n \rho_c \frac{4}{3} D_P^3 = \frac{(10)(2)(4)}{3} \pi D_P^3\)

\(D_P^3 = 0.1 \, \text{cm}^3\)

\(D_P = 0.46 \, \text{cm}\)

\(\text{Surface area} = n \pi D_P^2 = 10 \pi (0.46)^2 \, \text{cm}^2\)

\(= 6.77 \, \text{cm}^2\)

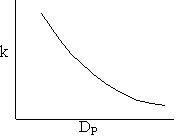
We see that for the same total weight of catalyst, the smaller diameter particles have a greater external surface area, and hence a grater rate constant per mass of catalyst.

Equation at bottom of DVD Chapter 12 page 829

\(-r_A = \frac{3}{R} \sqrt{D_e k_1} \, C_{AS}\)

\(-r_A = k C_{AS}\)

\(k = \frac{3}{R} \sqrt{D_e k_1} = \frac{6}{D_P} \sqrt{D_e k_1}\)


Diffusion limitations

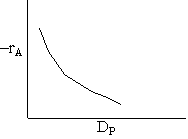
Graph showing the relationship between k and Dp with a downward sloping curve. The x-axis is labeled Dp, and the y-axis is labeled k.Graph depicting the relationship between -rA and Dp with a decreasing curve. The x-axis is labeled Dp, and the y-axis is labeled -rA.Graph showing the relationship between X and Dp, with a decreasing trend. The x-axis is labeled Dp, and the y-axis is labeled X.

Pressure drop limitations

     Laminar flow

Graph showing the relationship between α and D, where α varies inversely with D squared. The x-axis is labeled D, and the y-axis is labeled α.Graph showing the relationship between y (P/P₀) and Dₚ. The graph has a curve starting at the origin, increasing, and leveling off as Dₚ increases. The y-axis is labeled y = P/P₀, and the x-axis is labeled Dₚ.Graph depicting the relationship between X and Dₚ. The curve starts from the origin, rises steeply initially, and levels off as Dₚ increases. The y-axis is labeled X, and the x-axis is labeled Dₚ.

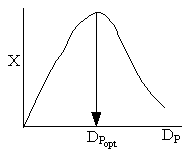
Combining diffusion limitation and pressure drop limitations as we change to particle size, we see there is an optimum particle diameter.

Graph showing the relationship between X and Dₚ with a peak at Dₚopt. The curve rises, reaches an optimal value (Dₚopt), and then decreases. The y-axis is labeled X, and the x-axis is labeled Dₚ.

Back to Chapter 5