Chapter 5: Isothermal Reactor Design: Conversion

Batch Reactor With a Reversible Reaction

The following reaction follows an elementary rate law

\(\text{N}_2 + \text{O}_2 \overset{k_1}{\underset{k_{-1}}{\rightleftharpoons}} 2\text{NO}\)

Initially 77% \(\text{N}_2\), 15% \(\text{O}_2\), and 8% inerts are fed to a batch reactor where 80% of the equilibrium conversion \((X_e = 0.02)\) is reached in \(151 \, \mu \text{s}\). What is the specific reaction rate constant \(k_1\)?

Additional Information

\(X_e = 0.02, \, V = 0.4 \, \text{dm}^3, \, K_C = 0.01, \, P = 20 \, \text{atm}, \, T = 2700 \, \text{K}\)

Solution

Mole Balance

\(\frac{dN_A}{dt} = r_A V\)

\(\text{Design Equation:} \, N_{A0} \frac{dX}{dt} = -r_A \cdot V\)

Rate Law

\(\text{N}_2 + \text{O}_2 \overset{k_1}{\underset{k_{-1}}{\rightleftharpoons}} 2\text{NO}\)

\(\text{A} + \text{B} \overset{k_1}{\underset{k_{-1}}{\rightleftharpoons}} 2\text{C}\)

\(-r_A = k_1 \left( C_A \cdot C_B - \frac{C_C^2}{K_C} \right)\)

Stoichiometry: Constant Volume

\(V = V_0\)

\(C_A = C_{A0} (1 - X)\)

\(C_B = C_{A0} (\Theta_B - X)\)

\(C_C = 2C_{A0} \cdot X\)

Combining

\(-r_A = k_1 C_{A0}^2 \left[ (1 - X)(\Theta_B - X) - \frac{4X^2}{K_C} \right]\)

\(\frac{N_{A0}}{V_0} \cdot \frac{dX}{dt} = -r_A\)

\(C_{A0} \frac{dX}{dt} = -r_A\)

Rearranging and Integrating

\(t = C_{A0} \int_0^X \frac{dX}{-r_A} = \frac{1}{k_1 C_{A0}} \int_0^X \frac{dX}{(1 - X)(\Theta_B - X) - \frac{4X^2}{K_C}}\)

Evaluate:

\(C_{A0} = \frac{y_{A0} \cdot P_0}{R \cdot T_0} = \frac{(0.77) \cdot (20 \, \text{atm})}{\left(0.082 \, \frac{\text{atm} \cdot \text{dm}^3}{\text{mol} \cdot \text{K}}\right) (2700 \, \text{K})}\)

\(C_{A0} = 6.96 \times 10^{-2} \, \text{mol}/\text{dm}^3\)

For 80% of equilibrium conversion X = 0.8 X_e = 0.016

\(\Theta_B = \frac{y_{B,0}}{y_{A,0}} = \frac{0.15}{0.77} = 0.195\)

\(\text{Solving for } k_1 \text{ and substituting for } C_{A0}, \, \Theta_B, \, t, \, \text{and } K_C \text{ gives}\)

\(k_1 = \frac{1}{\left(151 \times 10^{-6} \, \text{s}\right) (0.0696 \, \text{mol}/\text{dm}^3)} \times \int_0^{0.016} \frac{dX}{0.195 - 1.195 \cdot X - 399 \cdot X^2}\)

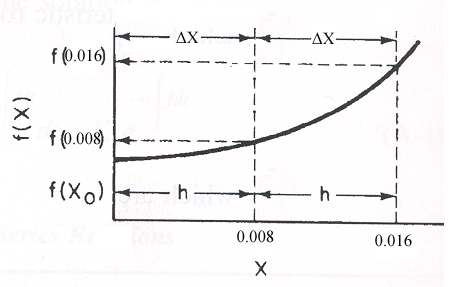
Use Simpson's three point formula to integrate with ΔX = 0.016/2 = 0.008

\(\int_{x_0}^{x_2} f(X) \, dX = \frac{\Delta X}{3} \left[ f(X_0) + 4f(X_1) + f(X_2) \right]\)

\(k_1 = 9.51 \times 10^4 \, \frac{\text{dm}^3}{\text{mol} \cdot \text{s}} \int_0^{0.016} f(X) \, dX\)

\(X_0 = 0, \, f(X_0) = 5.128\)

\(X_1 = 0.008, \, f(X_1) = 6.25\)

\(X_2 = 0.016, \, f(X_2) = 13.56\)

Simpson's rule: \((\Delta X = h = 0.008)\)

\(k_1 = 9.51 \times 10^4 \times \left(\frac{0.008}{3}\right) \left(5.128 + 4 \times 6.25 + 13.56\right)\)

\(k_1 = 1.11 \times 10^4 \, \frac{\text{dm}^3}{\text{mol} \cdot \text{s}}\)