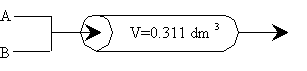Chapter 5: Isothermal Reactor Design: Conversion
Example 5.2: The Reaction From the Movie
The Laboratory Experiment
\((\text{CH}_3\text{CO})_2\text{O} + \text{H}_2\text{O} \rightarrow 2\text{CH}_3\text{COOH}\)
\(\text{A} + \text{B} \rightarrow 2\text{C}\)
\(\tau = \frac{1 \, \text{dm}^3}{0.0033 \, \text{dm}^3/\text{s}} = 303 \, \text{s}.\) A. CSTR A.1. Single CSTR
\(C_{A0} = 1 \, \text{molar A}\)
1. Mole Balance
\(\text{In - Out + Gen = Accum}\)
\(F_{A0} - F_A + r_A V = 0\)
\(V = \frac{F_{A0} - F_A}{-r_A} = \frac{F_{A0} X}{-r_A} = \frac{v_0 C_{A0} X}{-r_A}\)
2. Rate Law
\(-r_A = k' C_A C_B, \quad k' = 1.97 \times 10^{-4} \, \frac{\text{dm}^3}{\text{mol} \cdot \text{s}}\)
3. Stoichiometry Liquid v = v
\(\text{CH}_3 - \text{C} - \text{O} - \text{C} - \text{CH}_3\)
\( C_A = \frac{F_A}{\nu} = \frac{F_A}{\nu_0} = \frac{F_{A0}(1-X)}{\nu_0} = C_{A0}(1-X) \)
\( C_B = \frac{F_B}{\nu_0} = C_{A0}(\Theta_B - X) \)
\( \Theta_B = \frac{C_{B0}}{C_{A0}}, \quad C_{B0} \approx 51.2 \, \text{mol/dm}^3 \)
\( \Theta_B = 51.2 \)
\( \Theta_B = 51.2 \gg X \)
\( C_B = \Theta_B C_{A0} \equiv C_{B0} \)
4. Combine
\(-r_A = k'C_A C_B = k'C_{B0}C_A = kC_A\)
\(-r_A = kC_{A0}(1-X)\)
\(V = \frac{\nu_0 C_{A0} X}{kC_{A0}(1-X)}, \quad \tau = \frac{V}{\nu_0}\)
\(\tau k = \frac{X}{1-X}\)
\[
X = \frac{\tau k}{1+\tau k}
\]
\(k = k'C_{B0} = (1.97 \times 10^{-4} \, \text{dm}^3/\text{mol} \cdot \text{s})(51.2 \, \text{mol}/\text{dm}^3)\)
\(k = 0.01 \, \text{s}^{-1}\)
\(\tau k = 3.03\)
\[
X = \frac{3.03}{1+3.03} = 0.75
\]
A.2.
CSTRs in Series
\(F_{A1} = F_{A0}(1-X_1)\)
\(F_{A2} = F_{A0}(1-X_2)\)
\(\text{In} - \text{Out} + \text{Gen} = \)
\(F_{A1} - F_{A2} + r_{A2}V = 0\)
Balance on Second Reactor \(V_2 = \frac{F_{A0}(X_2 - X_1)}{-r_A}\) \(-r_{A2} = kC_{A2} = k\frac{F_{A2}}{v_0} = k\frac{F_{A0}(1-X_2)}{v_0} = kC_{A0}(1-X_2)\) \(V = \frac{v_0 C_{A0}(X_2 - X_1)}{kC_{A0}(1-X_2)}\) \(\tau k = \frac{X_2 - X_1}{1 - X_2}\) \(\tau k = X_2(1 + \tau k) - X_1\) \(X_2 = \frac{X_1 + \tau k}{1 + \tau k} = \frac{(0.75) + 3}{4.03} = \frac{3.75}{4.03}\) B. PFR 1. Mole Balance/Design Equation \(F_{A0} = \frac{dX}{dV} = -r_A\) 2. Rate Law \(-r_A = k'C_A C_B\) 3. Stoichiometry v = v0 \(C_A = C_{A0}(1 - X)\) \(C_B = C_{A0}(\Theta_B - X) \approx C_{B0}\) 4. Combine \(-r_A = k'C_A C_B = k'C_{B0}C_A = kC_{A0}(1 - X)\) \(\frac{dX}{dV} = \frac{-r_A}{F_{A0}} = \frac{-r_A}{v_0C_{A0}} = \frac{kC_{A0}(1 - X)}{v_0C_{A0}}\) \(\frac{dX}{dV} = \frac{k}{v_0}(1 - X)\) \(\frac{dX}{1 - X} = \frac{k}{v_0} dV\) \(V = 0, X = 0\) \(\ln\left(\frac{1}{1 - X}\right) = \frac{k}{v_0}V = k\tau\) \(X = 1 - e^{-k\tau}\) \(\tau = \frac{0.311 \, \text{dm}^3}{0.0033 \, \text{dm}^3/\text{s}} = 94.2 \, \text{s}\) \(k\tau = (94.2)(0.01) = 0.94\) \(X = 1 - e^{-0.94} = 0.61\) 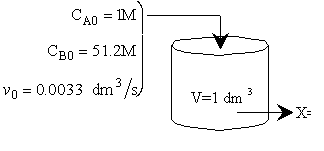 \(
\begin{aligned}
&C_{A0} = 1M,\\
&C_{B0} = 51.2M,\\
&v_0 = 0.0033 \, \text{dm}^3/\text{s}.
\end{aligned}
\)
\(
\begin{aligned}
&C_{A0} = 1M,\\
&C_{B0} = 51.2M,\\
&v_0 = 0.0033 \, \text{dm}^3/\text{s}.
\end{aligned}
\)
Species
Symbol
Entering
Change
Leaving
\(\text{CH}_3 - \text{C} - \text{O} - \text{C} - \text{CH}_3\)
A
\( F_{A0} \)
\( -F_{A0}X = F_{A0}(1-X) \)
\( F_{A0}(1-X) \)
\( \text{H}_2\text{O} \)
B
\( \Theta_B F_{A0} \)
\( -F_{A0}X = F_{A0}(\Theta_B - X) \)
\( F_{A0}(\Theta_B - X) \)
\( \text{CH}_3\text{COOH} \)
C
0
\( 2F_{A0}XF_{C} \)
\( 2F_{A0}X \)