Created by Susan Stagg-Williams, Dieter Andrew Schweiss, Gavin Sy, and H. Scott Fogler, 1994
Updated by Apeksha Bandi, Gustav Sandborgh, and Arthur Shih, 2013
Case 1: Worst Case Scenario
Introduction
You are lost in a jungle and suddenly get bit by a King Cobra after carelessly treading over a pile of old leaves. You are hours away from any civilization and don't have any antivenom on hand.
In this case, we will try to prove the claim that 85 to 90% of the fraction of free sites will be blocked
in half an hour. Remember that no antivenom will be injected to save your life. Cruel, aren't
we?
In addition to trying to prove the claim, we will also determine the twitch height threshold by
correlating the time it takes for 85 to 90% of the receptor sites to be blocked by venom to the value of the twitch height at that time.
To do this, we'll want to make use of Polymath.
Receptor Sites Analysis
The equations we'll enter into Polymath are based on the additional information given in the problem statement
and the equations derived earlier.
Code and Results
Our Polymath code for receptor sites analysis of Case 1 can be downloaded below:
Download the Code (.pol)
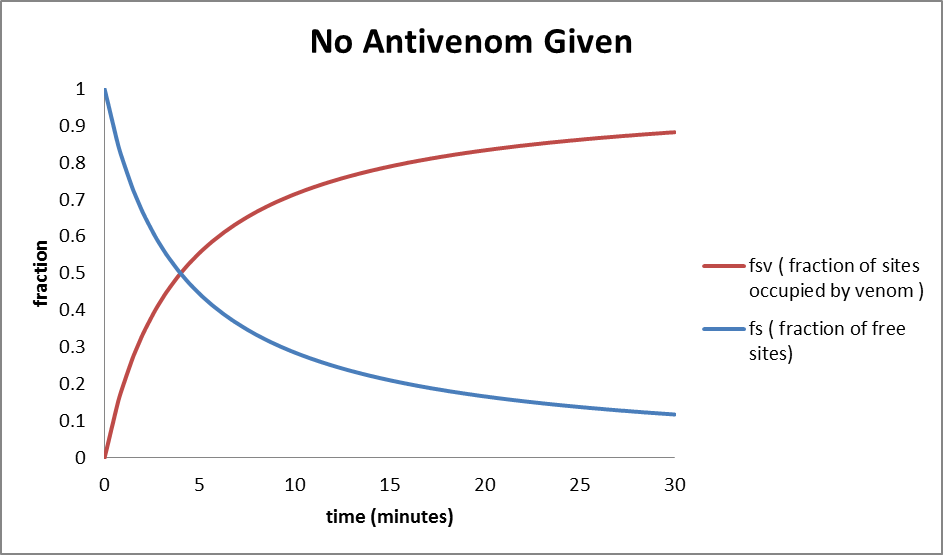
From the graph, we see that the fraction of free sites drops from 100 to 88.2% in 30 minutes.
This result confirms the fact that one would survive only for approximately half an hour after being bit by a cobra.
Twitch Height Analysis
We will now take a look at the effect of venom on twitch height. To review the theory and equations for twitch height, you can
return to the Equations page. To compute the values of twitch height , we will copy f
sv from Polymath's data table to a spreadsheet then compute twitch height from equation (E-40).
Code and Results
Our Polymath code for the Twitch Height Analysis for Case 1 can be downloaded using the links below.
Download the Code (.pol)
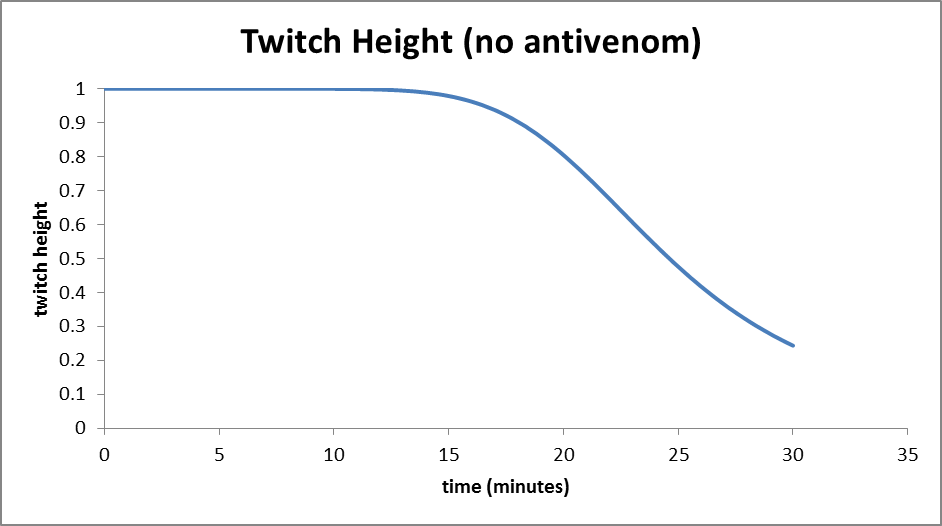
From the graph, we notice that the twitch height decreases to 0.243 half an hour after a cobra bite injection.
Since we already know that around 85 to 90% of free sites get blocked by then,
we conclude that the victim is at a risk of dying from suffocation when the twitch height drops below 0.243.

