
Tunnelling: Mechanics and hazards
Jim St. Marie

Introduction
A tunnel is a long, narrow, essentially linear excavated underground opening, the length of which greatly exceeds its width or height. (Walhstrom, 1973). In contrast, a cavern is an underground opening whoselength and width are roughly similar. These two types of excavations are end-members, and every underground excavation undertaken by mankind can be looked upon as a combination of the two. A shaft can simply be thought of as a tunnel which is vertical rather than horizontal.
For centuries, mankind has excavated caverns and tunnels in the earth for a myriad of uses. Historically, early man probably dug tunnels and caves for shelter, or to store food that had been killed or gathered. There is evidence that Stone Age people sank shafts and drove tunnels in order to obtain flint for bladed tools. (Wahlstrom, 1973) Later, as mankind developed the ability to make metal tools, the need to go underground for raw materials also developed, and more tunnels were dug. Early excavations in metal-bearing ores have been identified in Caucasia, near the Black Sea, which date back to about 3500 B.C. (Wahlstrom, 1973) Tunnels were built in ancient times by nearly every great civilization: Aztec, Inca, Babylonian, Egyptian, and Persian. The tools used in tunneling were the tools of the age: Bone, antler, flint and wood to the early humans, bronze, iron, and steel as civilization advanced. For centuries, tunnels in rock were driven by building fires against the rock faces, which would cause expansion and spalling, often accelerated by dousing the hot rock with water, then picking the fractured rock away with picks and wedges (Wahlstrom, 1973). Egyptian and Roman mines were worked to depths of approximately 200 meters. (Mahtab and Grasso) By the 6th century B.C., it has been estimated that the advance rate of a hand-worked tunnel in hard rock was perhaps 9 meters per year. (Beall, 1973) Today, nearly three thousand years later, the advance rate in a given excavation is increased over that by two or three orders of magnitude. (Mahtab and Grasso, 1992) The advent of explosives, first black powder, then nitroglycerine and dynamite, issued in a new age of excavation. Not just have the rates of excavation improved, however. Through improved methods of design and construction, the dimensions of underground workings have increased, and the modern underground worker can count on much greater safety and much better working conditions than an historical counterpart. With improvements in design and construction, the diversity of use has also widened, and tunnels are not simply the mines and shelters they used to be. Today, the human race excavates for transportation, mining, storage, defense, deposition of waste, and the list goes on. The primitive picks and wedges of the past have given way to the mechanized excavating tools, pneumatic drills, and sophisticated blasting methods.
The process of digging a tunnel in rock, however, is not simply a case of deciding where the tunnel is to go and then blasting one's way through. Rock is a very treacherous medium through which to travel. Even "solid" rock often contains innumerable cracks, faults, folds, and discontinuities, the activation of any of which may become a trigger to a collapse of the tunnel. The design and construction of a tunnel must account for the mechanical properties of the surrounding rock, which includes not only the aforementioned cracks and discontinuities, but also the weathering and deterioration of the rock, the number and type of layers in the rock, strike and dip of these layers, underground water level, overburden, and the list goes on and on. (Matsumoto and Nishioka, 1991) For this reason, the principles of mechanics are used to determine the feasibility, methods of design and construction, and the stability of the tunnel once it is excavated.
Tunneling is one of the most hazardous projects in engineering and construction.
It is also one of the most expensive. For this reason, extensive planning
and surveying goes into the pre-excavation stage of the project. Many years
often pass between the initial idea and the beginning of the excavation.
Figure 1, taken from Mahtab and Grasso (1992), is a flowchart showing the
general sequence of activities undertaken in tunnel design and construction.
Primary Concerns
First and foremost, there exist a number of general uncertainties and unknowns when dealing with the underground. These variables can range from minor inconveniences to major challenges to the designers of the tunnel. A short list of some of these concerns consists of: (Bickel, et al, 1996)
1. The overriding uncertainty when dealing with any underground project.
2. The geology of the area will determine the feasibility and the cost
of the undertaking.
3. Engineering properties of rock may change, sometimes drastically,with
a wide range of conditions, notably time, season, rate and direction of
loading.
4. Groundwater is the most difficult parameter to predict and the most
troublesome during construction.
5. Drilling core, the most common method of determining underground conditions,
only recovers less than 0.0005% of the excavated volume of the tunnel on
a typical project in the most exhaustive survey, which leaves a great deal
of room for uncertainty.
Site Characterization
Once the designers of the tunnel get down to the actual design phase, the first activity usually performed is a characterization of the site of the excavation. This involves characterizing the rock mass into which the tunnel is to be driven. This characterization will include the following properties: (Mahtab and Grasso, 1992)
1. Topography of the area, the climate and the accessibility of the
area.
2. Location of the cavity with respect to the ground surface and rock formation
boundaries.
3. Structural stability of the rock body, which is a function of seismisity,
faults, and stress concentrations.
4. Hydrologic regime and its perturbation, which is a function of the permeability
of the ground and the ground water flow rates.
5. Potential for subsidence and other surface effects.
6. Rock types in the rock mass, their genesis and their homogeneity.
7. Degree of weathering and weatherability of the rock.
8. Geologic discontinuities and other defects.
9. Deformability characteristics under short- and long-term loading.
10. Strength characteristics in reference to a rational failure criterion.
11. In-situ stress and hydraulic and/or dynamic loads.
12. Geometric and mechanical properties of systematic and extensive discontinuities.
Rock Mass Characterization
Put quite simply, the most important requirement that rock must fulfill when excavated is its ability to remain stable. Although this sounds simple, it is not always the case. Mahtab and Grasso (1992) define the term "rock mass" as the rock fabric and all the joints it contains. It is very important to consider the joints and cracks in a rock because, as mentioned before, these discontinuities can serve as a point of failure in a rock mass under stress.
Testing of the rocks in the area being considered for excavation is not always straightforward. There are a number of method for testing the rocks, both to determine the in-situ stress on the rock, as well as the rock's ability to withstand this stress. This second part often involves uniaxial and triaxial compression tests to determine the "strength" of the rock.
Tunnel engineers generally classify rocks on the basis of resistance to deformation (strength), amount of weathering, and general resistance to weathering. (Parker, 1996) These last two are not the same, although they may seem so at first glance. A rock may be very resistant to weathering, but may have also have been subjected to a very long period of time, which may result in significant weathering. In general, the strength and resistance to weathering of a rock is derived from the class of rock. Igneous and metamorphic rocks, in general, are more resistant to deformation and weathering than sedimentary rocks.
|
Class |
Descriptor |
Unconfined Stress |
Unconfined Stress |
|
R0 |
Extremely soft |
20-100 |
0.2-0.7 |
|
R1 |
Very low strength |
100-1000 |
0.7-7 |
|
R2 |
Low strength |
1000-4000 |
7-28 |
|
R3 |
Moderate strength |
4000-8000 |
28-55 |
|
R4 |
Medium high strength |
8000-16,000 |
55-110 |
|
R5 |
High strength |
16,000-32,000 |
110-220 |
|
R6 |
Very high strength |
>32,000 |
>220 |
|
Class |
Descriptor |
Definition |
|
W1 |
Fresh rock |
No visible signs of weathering. Any breaks are across sound rock |
|
W2 |
Slightly weathered |
Slight discoloration and minor weakening of the rock material |
|
W3 |
Moderately weathered |
Fresh rock is still present, but up to 50% of the rock material has been decomposed into soil |
|
W4 |
Highly weathered |
Fresh rock is still present, but more than 50% of the rock material has been decomposed into soil |
|
W5 |
Completely weathered |
All of the rock material has been decomposed into soil, but the original rock mass structure has been preserved |
|
W6 |
Residual soil |
All of the rock material has been decomposed into soil, and there has been transport, and all original structure has been destroyed |
Although the classifications in these two tables are quite simple, the descriptions of rock masses can be extremely complex, and are much more so than for soils. The reason for this is that, although rocks have a greater innate strength than a soil, their mechanical characteristics are dominated by the effect of anisotropy (the state of a characteristic of the rock being different in different directions) and the discontinuities contained within. These discontinuities may range from foliation in the rock , such as the layering in a schist or the fissibility of a shale. The discontinuities may also take the form of fractures, ranging from the minuscule cracks to major faulting. (Parker, 1996)
Few tunnels are excavated without the use of some kind of artificial support. Terzaghi (1946) developed a classification scheme to describe rocks and their load on steel supports. Although this classification scheme is fifty years old, and is limited with today's technology, the classification scheme it is still quite useful for basic descriptions. Terzaghi's seven rock mass descriptions are as follows: (Terzaghi, 1946)
Intact rock: Intact rock contains neither joints nor hair cracks, and thus breaks across sound rock. Spalling conditions, which is when thin slabs of rock fall off the roof or walls of the tunnel, , and popping conditions, where rock slabs on the sides or roof of the tunnel spontaneously and violently detach, may occur for several hours or days after blasting.
Stratified rock: Stratified rock consists of individual strata with little or no resistance against separation along strata boundaries. Spalling conditions are quite common.
Moderately jointed rock: Moderately jointed rock contains joints and hair cracks, but blocks between the joints are locally grown together or so intimately interlocked that vertical walls do not require lateral support. Again, spalling and popping conditions may be encountered.
Blocky and seamy rock: This consists of chemically intact or nearly intact rock fragments which are entirely separated from each other and imperfectly interlocked. The vertical walls of the tunnel may require support.
Crushed rock: Crushed rock is chemically intact, but extensively fractured. If the crushed rock is small-grained and below the water table, it will exhibit the properties of a water-bearing sand.
Squeezing rock: Squeezing rock slowly advances into the tunnel without a perceptible volume increase. This condition requires a very high percentage of microscopic and submicroscopic micaceous minerals or clay minerals with a low swelling capacity.
Swelling rock: Swelling rock advances into the tunnel primarily by the expansion of the rock itself. This condition seems to be limited to rocks containing clays, such as montmorillonite, which have a high capacity to swell when hydrated.
Rock mass classification schemes abound, and nearly every different author has a different method of classifying rock masses for excavation purposes
Tunnel Geometry
In the design of tunnels, designers attempt to utilize a shape that will prove the most stable. Basic mechanics, in conjunction with the rock mass classification, dictates the most effective geometry. For instance, tunnels are rarely excavated with a flat roof. The reason for this is that, as the span increases, the rock in the center has less force holding it up, and a flat-roofed tunnel is more susceptible to collapse. However, when tunnelling is strongly stratified rock, such as shale, the roof is often cut flat, taking advantage of the rock's natural tendency to break along bedding planes. By cutting the tunnel along bedding planes and then supporting the roof, the tunnel would be less apt to collapse than if a different geometry were employed which cut across the bedding of the rock, making it more unstable. (Wahlstrom, 1973) For the most part, however, tunnels are excavated with roofs that are circular segments, which is the most stable geometric shape with regard to an externally-applied stress. Also common are tunnels cut with horseshoe shapes, or tunnels with gothic arch roofs, which provide maximum stability in the roof section. (Wahlstrom, 1973)
In addition to the shape of the tunnel section, the size is also very
important. It is generally considered that the minimum size for a tunnel
that will still permit reasonable working space is at least 7 feet (2.15
m) high by 4 feet (1.2 m) wide, clear of the wall or the supports, for
a walkway. (Wahlstrom, 1973) For obvious reasons, any tunnel designed for
vehicle traffic would have to be larger. The primary problem in sizing
a tunnel is one of support against external stress. Consider circular tunnels:
Using the formula of (pi)r2 to calculate the area of a circle
(or in this case, an infinitesimally thin slice through a circular tunnel),
it can be shown that doubling the diameter (2r) of a circular tunnel results
in four times the area (2r) of the slice. This means that doubling the
diameter of a tunnel requires removing four times as much rock. This rock,
up to the point of excavation, had been in equilibrium with the surrounding
rock, and had been supporting it. In addition, the surface area of the
tunnel is doubled, and so the forces in the rock which are trying to bring
down the tunnel are now acting over twice as large an area. It is for this
reason that the use of supports is much more important in larger tunnels
than in smaller ones. Often, in cases where tunnels are to be driven into
rock of questionable competence, very small tunnels are driven first and
then carefully enlarged and supported during the enlarging process. (Wahlstrom,
1973)
The Mechanics of it all
First of all, it is not possible to cover all of the mechanics of tunnel design and construction in a short paper. Dozens of books hundreds of pages long have been devoted to this. However, there are a few basic concepts which apply to the design process, and I will cover those, then a brief description of the tunnel design process itself..
The two concepts in mechanics which most apply to tunnelling are stress and strain. Stress may simply be thought of as a force applied on a body, and strain may simply be thought of as that body's deformational response to the stress. For instance, consider placing a heavy book on top of a grape. The stress is the force of gravity and the mass of the book, and the strain is the reaction of the grape to the stress, namely, flattening. Staining of the book by the grape juice is a chemical process, and is not considered in this paper. Stress and strain models are used by most tunnel engineers to determine the feasibility of a particular excavation. However, recent models have begun to move away from a stress-and-strain focus. The focus of some of the newer models is the distortional strain energy stored in the rock masses. The reason for this is that energy is a scalar, and thus has no direction, so that the analysis may be performed without regard to the directions of the stress and strain acting on the rock body. (Matsumoto and Nishioka, 1991) However, this paper will not go into the discussion of these methods, primarily because they have not been tested to the extent of the classical mechanics models, and also because the author has difficulty understanding them.
In the consideration of stress and strain, the dynamic nature of a material can be put into three classes of ideal behavior, and all real materials behave in some combination of the three.
1. Hookian solid-body (elastic) behavior: In elastic behavior, the strain is completely proportional to the stress applied, so that a plot of stress vs. strain yields a straight line.
2. St. Venant's solid-body (plastic) behavior: In plastic behavior, an applied stress will not result in any strain until a certain stress is reached (yield point). At this point, only strain increases. Reduction of the stress to below the yield stress will result in the cessation of the strain.
3. Newtonian liquid (viscous) behavior: In viscous behavior, the rate of strain is proportional to the stress applied. That is, as the stress applied increases, the deformation does not increase, but the rate at which the body deforms does.
With respect to these three ideals, no rock behaves perfectly in these manners, but rather in some combination of elastic, plastic, and viscous. A potentially important quality of some materials, notably glasses, is fragility. A material exhibiting fragile behavior will shatter while still in the range of elasticity. (Matsumoto and Nishioka, 1991). However, many materials which would normally behave in a fragile manner while being compressed from one direction will flow in a ductile manner when compressed from all three directions. (Matsumoto and Nishioka, 1991)
The term "rock strength" is comprised of a number of different types of properties. Rocks are often tested for strength by use of a uniaxial compression test, in which a cylinder of rock is placed in a vise and compressed along its length. This is a measure of compressive strength. Other tests may measure tensile strength (the rock's ability to withstand being pulled apart), flexural strength (the ability to withstand bending), unconfined shear strength (the rock's ability to withstand being cut in two), or triaxial compressive strength. In triaxial compression tests, the rock is confined in a pressurized fluid, which compresses it, imitating the confining pressure of rock at depth. In these triaxial tests, the failure pressure of the rock is normally quite higher than under uniaxial stress. During the triaxial compression test, if even a slight sideways pressure is imposed on the rock, a shear failure occurs. (Matsumoto and Nishioka,1991) The greater the confining pressure on the sides, the greater the maximum stress at failure, and the less failure that will occur. One curious phenomenon in some rocks is that of strain hardening. Certain plastic or ductile materials may, when subjected to a certain degree of deformation, develop increasing strength. This is occasionally observed in underground openings, especially when plastic rocks with low initial strength become stiffer and more resistant to strain dislocation after a period of time (Wahlstrom, 1973)
Rocks around a tunnel are considered to be under triaxial compression. This leads to a very dangerous problem: If the rocks are under triaxial compression, and the confining rock on one side is removed as the tunnel is driven, there will exist a severe stress gradient on the rocks. The rocks which make up the tunnel wall and roof will be subjected to high stresses on the one side, but the counteracting force is no longer present, as those rocks are no longer present. This situation can, in deep mines, lead to rock bursts, where large portions of the tunnel walls can suddenly and violently explode in seismic events which are often measured at -2 to 4 on the Richter scale (Jha and Chouhan, 1994)
So where does this bring us? The actual three-dimensional mathematical
modeling of the design of a tunnel is a very complicated process, involving
a fair amount of differential equations. For instance, a three-dimensional
model would contain the three normal strains, the three shear strains,
the three normal stresses, the three shear stresses, and the three deformations
or displacements measured in Cartesian space. These fifteen unknowns can
translate into 36 elastic constants. (Mahtab and Grasso, 1992) However,
by making a very simple assumption, it is possible to use a two-dimensional
mathematical model, which greatly simplifies the process and works quite
well. The basic assumption made is that all the stresses involved are either
in or parallel to the plane of interest (xy, for example). There are a
number of different solutions out there, but a good number of them make
use of the following assumptions: (from Mahtab and Grasso, 1991)
1. stressz =shear strainxz = shear strainyz
= 0
normal strainz =0
where the subscript denotes the direction of stress or strain
The inverse Hooke's law (strain-stress relations) are derived and are:
normal strainx = 1/E(stressx-PR*stressy)
normal strainy = 1/E(stressy-PR*stressx)
shear strainxy = shear stressxy/G
normal strainz = (-PR/E)(stressx+stressy)
where:
PR is the Poisson's ratio (ratio of contraction and expansion = -epsilon1/epsilon3
E is the Young's modulus (ratio of stress and strain = sigma/epsilon)
G = E/2(1+PR), which is one of the Lamé constants.
The Hooke's Law for plane stress is given by the inversion of the above equations:
stressx = (E/1-PR2)(strainx+PR*strainy)
stressy = (E/1-PR2)(strainy+PR*strainx)
shear stressxy = G*shear strainxy
Plane strain can be illustrated by a long, cylindrical opening, which is conveniently what a tunnel is. If z represents the axis of the opening, the displacements of all the points in the plane of the cross-section (x-y) plane are not zero, but the shear strains
associated with the z direction are zero (shear strainyz =shear strainzx = 0) and strainz must be constant (and is usually set equal to zero for convenience). With the conditions thus, the Hooke's Law becomes:
stressx = (L + 2G)strainx+L*strainy
stressy = (L + 2G)strainy+L*strainx
shear stressxy = G*shear strainxy
where:
G = E/[2(1+nu)]
L= PR*E/(1+PR)(1-2PR), which is the second Lamé constant
As a result, the stress in the z direction (the constrained slice of tunnel) is given by:
stressz = PR(stressx+stressy)
And, for the strain-stress relations for plane strain, we have:
strainx = 1/E[(1-PR2)stressx -PR(1
-PR)stressy]
epsilony = 1/E[(1-PR2)stressy -PR(1-PR)stressx]
shear strainxy =shear stressxy/G
Thus, using the above equations, in conjunction with rock mechanics testing and perhaps in-situ testing of the stress conditions underground, the tunnel engineer could approximate the existing stresses on the rocks at depth, and can estimate the potential strains which may result from excavating a tunnel. From these, the engineer can determine the following:
1. The feasibility of the project, given the rocks' potential to remain
competent.
2. The costs of the project, in terms of time, labor, and structural support.
3. The type and amount of artificial support needed for stability.
4. The optimum geometry for the tunnel, based on rock qualities.
Problems
These equations, are theoretical. Nature, unfortunately, has an ability to and a habit of throwing kinks into well-laid plans. This section will demonstrate a number of difficulties associated with excavation.
When any underground excavation is made in an already weak rock, it often serves to further weaken the rock above it. This is due to a combination of 1) the excavation activity itself (primarily blasting) weakening the surrounding rocks as a result of shock waves and 2) the removal of supporting rock from underneath a large mass of rock. The net effect of this, weakening of rock and also giving it a place to go, is a movement toward the tunnel from above, which wraps around the tunnel and forms wedges of material which press in on the sides of the tunnel (Terzaghi, 1946) As Figure 4 illustrates, the rock in area abcd, loosened by the excavation, is attempting to move downward, and is being resisted by friction on surfaces ac and bd. The effect of this is the transfer of a large amount of the overburden, W1, onto the abutments of the tunnel. This tunnel will require steel supports, and they will be supporting a load equivalent to Hp, which will depend on the characteristics of the rock mass and the dimensions of the tunnel.
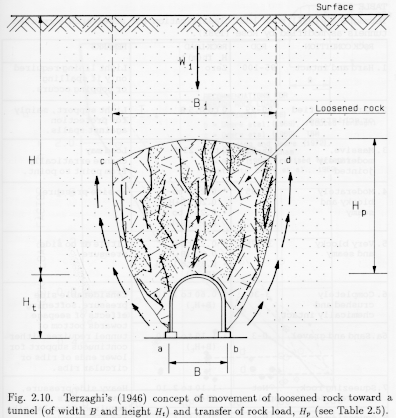
Figure 4. Movement of loosened rock toward a tunnel
As was mentioned earlier, tunnels are sometimes cut with flat roofs when excavated in strongly laminated rock, in order to take advantage of the rock's tendency to separate on those planes. However, it is rarely the case that laminated rocks are found in a pristine state with their bedding planes parallel and horizontal. Inclined bedding planes in stratified rocks pose a great problem, in that there is a great tendency for the rock to move along the bedding planes and thus slide into the tunnel, as as indicated in Figure 5, modified from Terzaghi (1946). The steep angle of the bedding planes with respect to the tunnel will result in the wedge-shaped rock body (aed) sliding into the tunnel and putting stress on the support (ac). The lateral force, P, can be estimated from the mass of the sliding rock body and the angle which it makes with the tunnel support. According to King (1996), the load on the tunnel and supports depends on the strike and dip of the strata, and tunnels will have to be cut more narrowly in the event of steeply inclined stratified rocks.
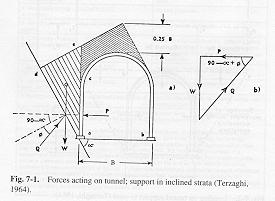
Figure 5. Forces acting on a tunnel in inclined strata
In general, rocks have a high resistance to crushing. King (1996) states that the walls of a tunnel will not fail as a result of compression except at great depth - more than 2000 feet (600 m) for softer sandstones and more than 19,000 feet (5800 m) for the strongest rocks. However, the rocks are still under an immense amount of stress, and the rock left standing after tunnel or cavern excavation must bear a greater load than before, as illustrated in Figure 4 from Terzaghi. This point is further illustrated in Figure 6, from Herget (1988). The grid lines represent the principal plane-strain stresses around a circular tunnel after excavation. The crowding of the trajectories at the sides indicates an increase in compression, and the widening at the top and bottom indicates a decrease in compressive stress. This implies that the walls of a tunnel, not the roof, would be more susceptible to failure. This is the mechanical basis of the rockburst phenomenon.
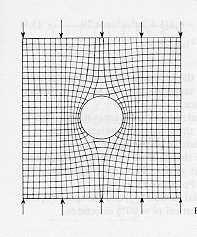
Figure 6. Deflection of stress around a circular opening
Of all the hazards associated with mining, rockbursts are perhaps the most terrifying. A rockburst is the sudden, violent dislocation of slabs of rock in a tunnel, usually from the walls, but also potentially from the roof or even floor. Considered to be a "mining-induced seismic event," a rockburst can release enormous amounts of energy, and some have been measured at 4 on the Richter scale (Jha and Chouhan, 1994) and one rockburst was recorded by a seismological station 1200 miles distant. (Obert and Duvall, 1967) The danger is obvious and quantifiable: In a three-year period in the Kolar gold-field in India, rockbursts accounted for 50% of all fatalities. (Obert and Duvall, 1967) The above link (blue "rockburst") illustrates the before and after of a rockburst in the Kolar gold-field. (Whittaker, et. al., 1992)
What are the causes of rockburst? One of the primary causes is obviously stress. The forces necessary to shatter tons of rock require the input of stress. The other primary factor is the rock type. An interesting point about rock bursts is that they do not occur in weak rocks. It is thought that the pressures which can cause a rockburst are slowly released in the weaker rocks by semiplastic adjustments. (Wahlstrom, 1973) The rocks affected are nearly always hard, strong, and brittle. These rocks may have an unconfined compressive stress of 15,000 to 60,000 psi (100-400 MPa) and a Young's modulus (modulus of elasticity) of 6x10^6 to 14x10^6 psi (40,000 to 90,000 MPa) (Obert and Duvall, 1967) In the United States, the most common location for rockburst phenomena seems to be the Coeur d'Alene mining district of northern Idaho, where the galena mines run over a mile deep into the quartzites of the Revett Formation of the Belt Supergroup.
Mathematically, it can be shown that the strain energy per unit volume, defined as the (normal stress)2/2E, where E is the Young's modulus, or the ratio of stress to strain. The maximum strain energy per unit volume would be C0/2E, where C0 is the uniaxial compressive stress. (Obert and Duvall, 1967) All other things being equal, the weakest rocks would be the least likely to burst, because they would reach their failure point far before they could store enough strain energy to produce a violent failure.
It appears that the lithostatic pressure of depth is not in general sufficient to produce the amount of stress necessary for a rockburst. What appears to also be required is a mechanism for producing a localized increase of the stress of the rock. The possibilities are numerous, including dike intrusion, faulting, and many others. Figure 7, taken from Wahlstrom (1973), illustrates three of the many possibilites. The quartzites of the Revett Formation in the Coeur d'Alene mining district are stressed by a myriad of faults, two of which (the right-lateral strike-slip Osburn and Placer Creek faults) trace for over 100 kilometers. (Wallace, et. al., 1980, Swanson, 1992)
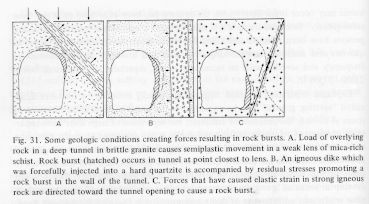
Once the major conditions are met, rockbursts still require a mechanism for failure. Germanovich, et. al. (1994) and Nemat-Nasser and Horii (1982) describe a mechanism by which a crack, initially inclined to the principal stresses, will grow in the direction of the principal stresses. This so-called "crack kinking" is shown in Figure 8 below, with both an inclined crack which has kinked as well as a pore which has begun cracking under stress.
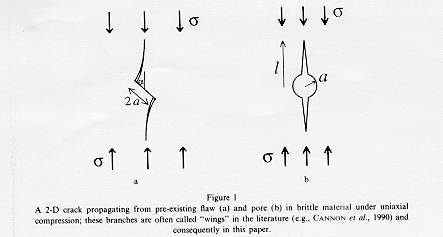
Figure 8. Cracks propagating from a) pre-existing flaw and b) pore
In the presence of a free surface (in this case, the tunnel wall), the cracks growing parallel to the free surface are affected by the free surface, and grow unstably after reaching a certain length. (Dyskin and Germanovich, 1993a) This instability of crack propagation can result in the separation of thin layers of rock from the rock mass and produce spalling. (Germanovich, et. al., 1994) In a way, each individual crack can be looked upon as a stress concentration. By itself, a single crack probably won't be responsible for a failure, but through the stress-induced crack growth, interaction of the cracks may cause the rock to reach a level of instablility where it will fail.
As observed by Nemat-Nasser and Horii (1982) in their experiments with compression of resin, the presence of a free surface had the effect of inducing crack-kinking away from the free surface. The cracks then followed (more or less) the free-surface contour. In rock, this would have the effect of forming slabs of rock parallel to the wall, which may then buckle or explosively break in a rockburst. (Nemat-Nasser and Horii, 1982) click here to see it
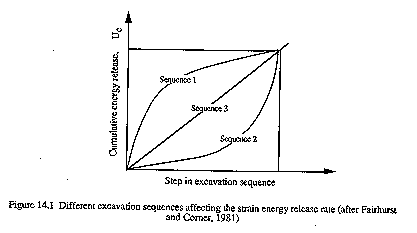
Rockbursts are, however, mining-induced events. Were it not for the removal of rock, the rock mass would stay perfectly happy at depth. Excavation causes a large stress gradient and the potential for release of the rock's stored strain energy. The rate of release of the strain energy is important. A gradual release may be perfectly safe, whereas the violent releases of energy are what we call rockbursts. Figure 9, taken from Whittaker, et. al. (1992) illustrates three different excavation sequences. Sequences 1 and 3 both result in the release of energy quickly, which makes them more susceptible to rockburst than Sequence 3, which has a more uniformly gradual release of energy. A great deal of mining research is directed toward techniques which will allow the gradual release of strain energy in rocks, and thus avoid rockburst.
Conclusion
Excavation of tunnels in rock is a complicated, dangerous, and expensive process. The mechanics of this can be very complex. However, in the case of excavation into rock which has a certain degree of competence, approximations can be made that will allow for simplification of the mathematics, at least in the preliminary design phase, which will allow for the simple calculation of the feasibility of the project. In the actual design of the tunnel, the more complex mathematical models would be used, and with a number of computer application programs, be much quicker and more accurate than in the past, ensuring the excavation of a safe and stable tunnel.
References
Barton, N., Lien, R., Lunde, J., 1974, Engineering classification
of rock masses for the design of tunnel support, Rock Mechanics,
v. 6, no. 4, pp. 189-236.
Beall, J.V., 1973. Mining's place and contribution. In: Cummins and Given
(Editors), SME Mining Engineering Handbook. AIME, New York, Vol.
1:1-2 to 1-13.
Bickel, J.O., Kuesel, T.R., and King, E.H., 1996, Tunnel Engineering
Handbook (Second Edition), Chapman & Hall, 544 pages.
Bieniawski, Z.T., 1973, Engineering classification of jointed rock masses, Transactions of the South African Institution of Civil Engineers, v. 15, pp. 335-344.
Bieniawski, Z..T., 1992, Design Methodology in Rock Engineering, A.A. Balkema, 196 pages.
Cha, P.C., and Chouhan, R.K.S., 1994, Long Range Rockburst Prediction: A Seismological Approach, International Journal of Rock Mechanics, Mineral Science, and Geomechanical Abstracts, vol. 31, No. 1, pp. 71-77
Germanovich, L.N., Salganik, R.L., Duskin, A.V., and Kee, K.K., 1994, Mechanisms of Brittle Fracture of Rock with Pre-existing Cracks in Compression, Pageoph, Vol, 143, No. 1/2/3
Herget, G., 1988, Stresses in Rock, A.A. Balkema, 179 pages
King, E.H., 1996, Rock Tunnels, Tunnel Engineering Handbook, Bickel, J.O., Kuesel, T.R., and King, E.H., eds., second edition, Chapman & Hall, pp122-152.
Mahtab, M.A., and Grasso, P., 1992, Geomechanics Principles in the Design of Tunnels and Caverns in Rocks, Elsevier Press, 250 pages.
Matsumoto, Y., and Nishioka, T., 1991, Theoretical Tunnel Mechanics,
University of Tokyo Press, 223 pages.
Obert, L., and Duvall, W.I., 1967, Rock Mechanics and the Design of
Structures in Rock, John Wiley & Sons, 650 pages.
Parker, H.W., 1996 Geotechnical Investigations, in Tunnel Engineering
Handbook, Bickel, et al (eds).
Terzaghi, K., 1946, Rock defects and loads on tunnel supports, Rock tunneling with steel supports, Proctor, R.V., White, T.L., and Terzaghi, K., editors, Commercial Shearing and Stamping Co., Youngstown, Ohio.
Walhlstrom, E. E., 1973, Tunneling in Rock, Elsevier , 250 pages
Whittaker, B.N., Singh, R.N., Sun, G., 1992, Rock Fracture Mechanics; Principles, Design, and Applications, Elsevier, 570 pages.
Williams, T.J., Wideman, C.J., and Scott, D.F., 1992, Case History of a Slip-Type Rockburst, Pure and Applied Geophysics, v. 139, 3-4, pp. 627-637