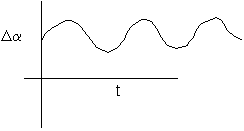
Oscillating Reactions Web Module
In this section we will carry out a linearized stability analysis of the reactions just discussed to determine the start and end time of the oscillations, the frequency, and the number of oscillations. Even though an abbreviated form of the BZ reaction is given on the web below, it is still relatively complex. Consequently to illustrate how oscillating reactions occur we shall use the following relatively simple reaction sequences. Consider the following elementary multiple reactions.
(1)
![]()
![]()
(2)
![]()
![]()
(3)
![]()
![]()
(4)
![]()
![]()
Batch mole balances and combined rate laws
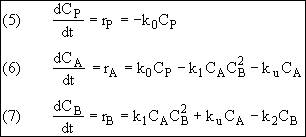
The initial conditions are that when t = 0 then: CP = CP0 and CA0 = CB0 = 0
![]()
Concentration
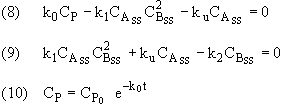
Solving for the pseudo-steady state concentrations
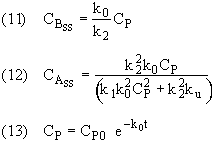
We will now put the equations in Dimensionless form by
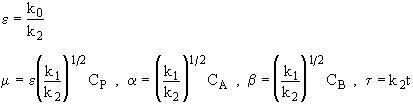
then
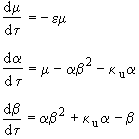
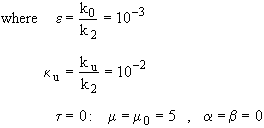
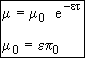
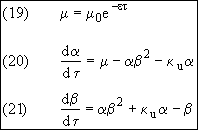
![]()
|
In terms of dimensionless variables
|
|
At
tcross
(27)
![]()
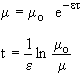
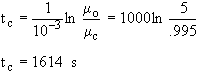
At tmax
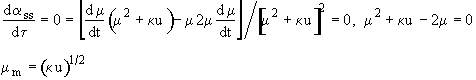
(28)
![]()
![]() reaches a maximum at
reaches a maximum at
![]()
Recall the dimensionless form of the combined mole balances and rate law is:
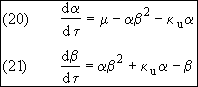
(29)
![]()
(30)
![]()
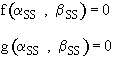
Let Da and Db be perturbations from the pseudo-steady state.
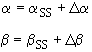
We will now substitute for a and b and expand f(a,b) and g(a,b) in a Taylor series around the Pseudo Steady State values ass and bss.
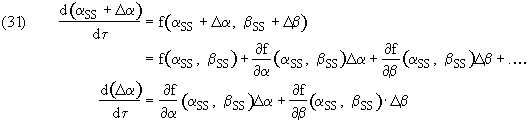
By recalling f(ass,bss) and g(ass,bss) are zero
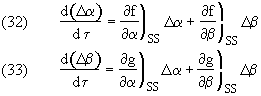
Then,
Where,
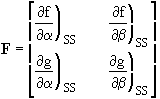
For which the solution to Equations (32) and (33) is
(36)
![]()
(37)
![]()
where the roots of the solution matrix are
(40)
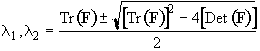
Hopf
Bifurcation
The real part of l1, l2 is zero, i.e. Tr(F) = 0
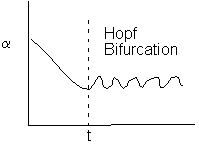
An exchange of stability from a stable critical point to a limit cycle, a bifurcation of this type, from an equilibrium to a periodic solution is called a Hopf bifurcation.
For oscillating behavior, Tr(F) = 0
recalling
(41)
![]()
and
(42)
![]()
and
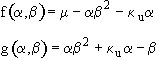
we now evaluate the expansion terms in the Taylor series
(43)
![]()
(44)
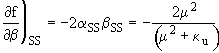
(45)
![]()
(46)
![]()
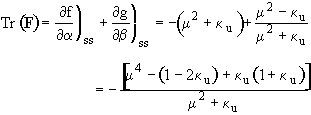
(2)
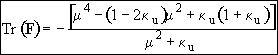
We will now evaluate the determinate
Det
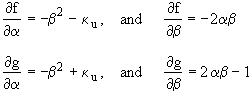
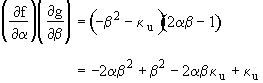
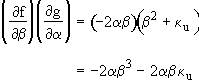
DET ![]()
![]() , however, for PSSH, bSS
= m
, however, for PSSH, bSS
= m
Det (F) = m2 + ku / QED
![]()
We now want to consider the case where we have pure oscillations, Tr(F)=0
Setting
![]() we find
we find
![]()
Solving for the roots which will make Tr=0, and produce pure oscillation
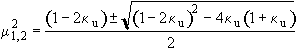
(48)
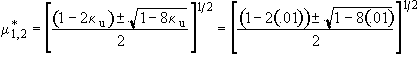
where m1,2
are the roots of the equation with
![]() taking the + sign
taking the + sign
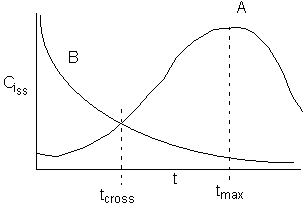
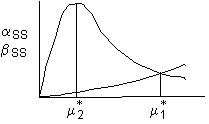
Find the start and end of oscillations
The oscillations begin when m = m1* and end when m = m2*
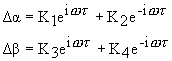
We can now calculate the times at which the oscillations begin and end.
![]()
we see that we start at t=0
and m=mo
and that m
decreases with t
(time). The oscillations start at when m
reaches
![]() . The corresponding dimensionless time is
. The corresponding dimensionless time is
![]()
The oscillations end when m
reaches
![]() .
.
![]()
The figure below shows how the roots vary with ku.
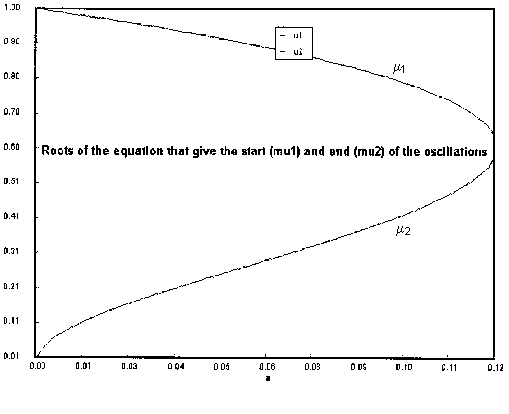
![]()
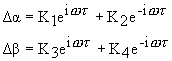
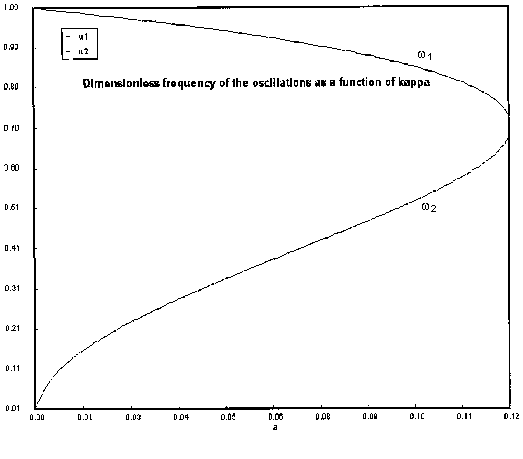
The dimensionless frequency of oscillation is
![]()
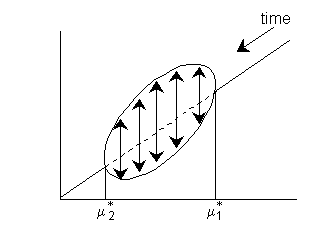
The figure below show the frequencies of oscillation near the start
![]() and end
and end
![]() of the oscillations as a function
of ku.
of the oscillations as a function
of ku.
Finding the periods of the oscillation
The dimensionless period of the oscillation
![]()
At the start of the oscillations
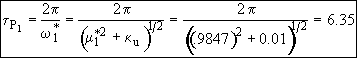
![]()
![]()
Near the end of the oscillation
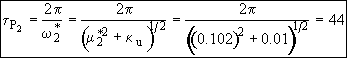
![]()
The figures below shows the dimensionless periods of oscillation,
![]() and
and
![]() as a function of ku.
as a function of ku.
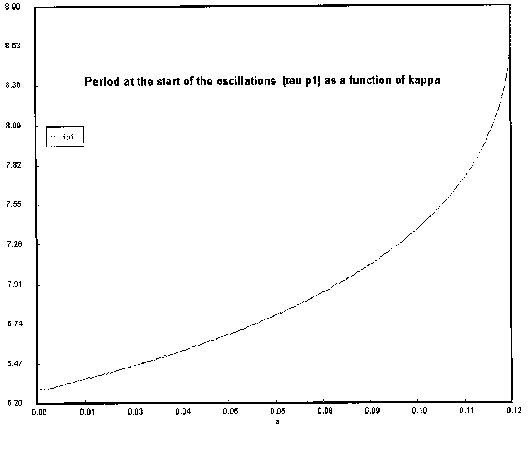
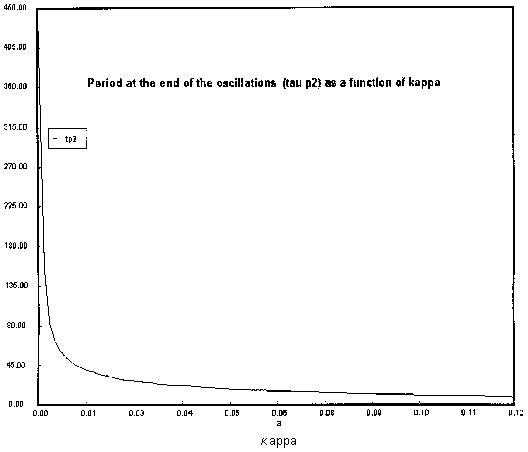
The geometric mean period of oscillation
![]()
![]()
The time of the oscillation is
![]()
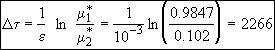
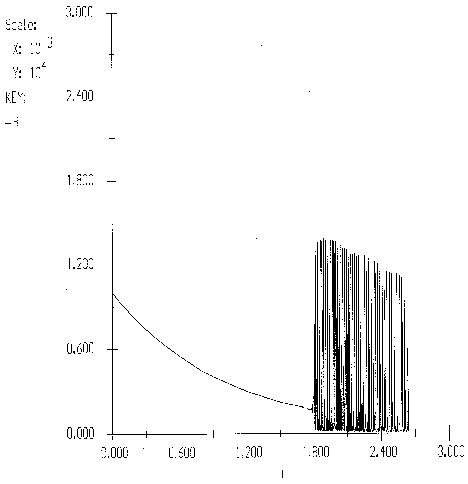
![]()
The number of oscillations
![]()
Dimensionless mean frequency of oscillation
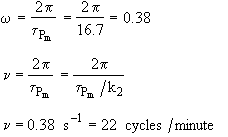

2) Oscillating Reactions
(1) Under what conditions would the time at which oscillations begin (e.g. t = 1800s) increase as the temperature increases by 10°C?
(2) Under what conditions would the time at which the oscillation begin and end remain the same?
(3) Under what conditions would the period of oscillation in seconds at both the start and end of the oscillation time decrease with increasing temperature?
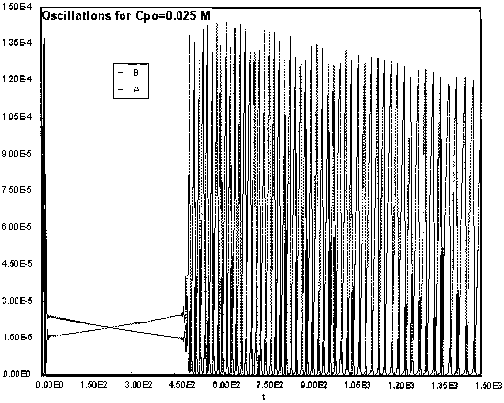
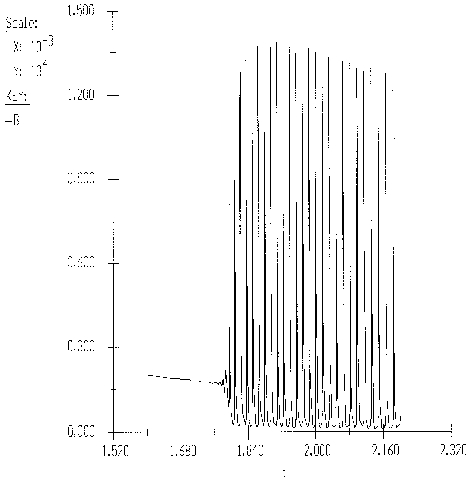
Adapted from Chemical oscillations and Instabilities, by Peter Gray and Stephen K. Scott, Oxford Science Publications, 1990.
Two coupled ODEs
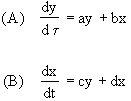
Click back (page 4 Oscillating Reactions)
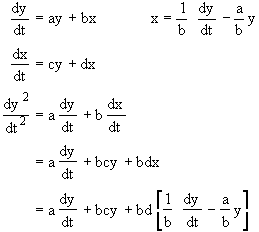
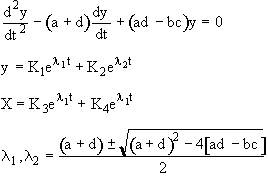
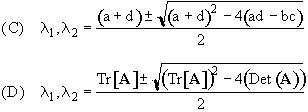
Determining
the properties of the roots l1,
l2
1. If Tr(F) < 0 , Det (F) > 0 , [Tr2(F) – 4 Det(F)] > 0
Both l1 and l2 are real and negative
Critically Damped
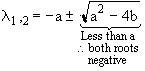
2. Tr(F) < 0 , Det (F) > 0 , [Tr2(F) – 4 Det(F)] < 0
![]()
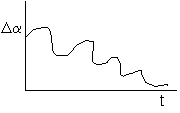
3. Tr(F) > 0 , Det (F) > 0 , [Tr2(F) – 4 Det(F)] < 0
Unstable oscillations
![]()
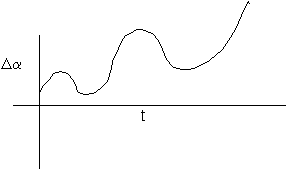
4. Tr(F) > 0 , Det (F) > 0 , [Tr2(F) – 4 Det(F)] > 0
![]()
Both roots positive + and real
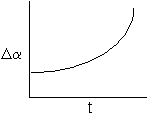 unstable
unstable
5. Tr(F) = 0 , Det (F) > 0 ,
![]() ,
,
![]()
![]() ,
,
![]()