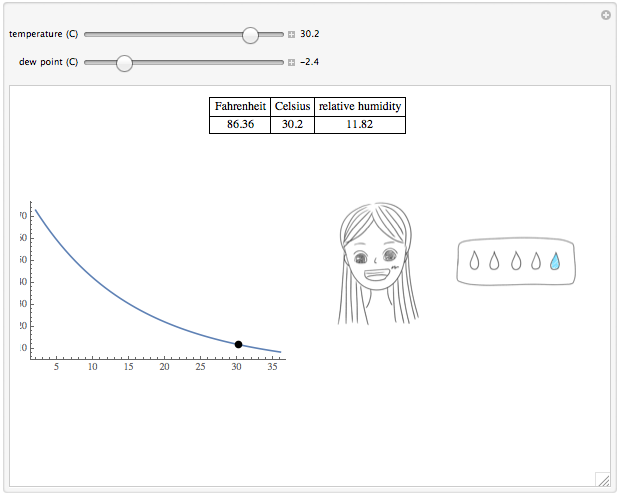
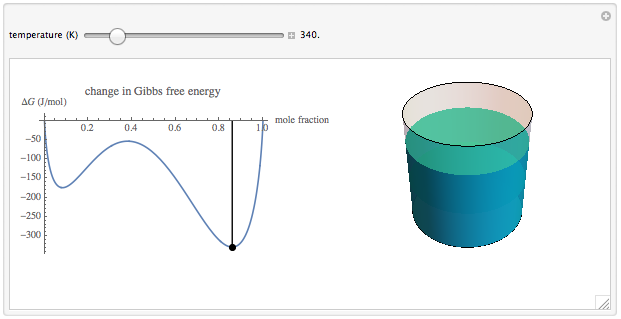
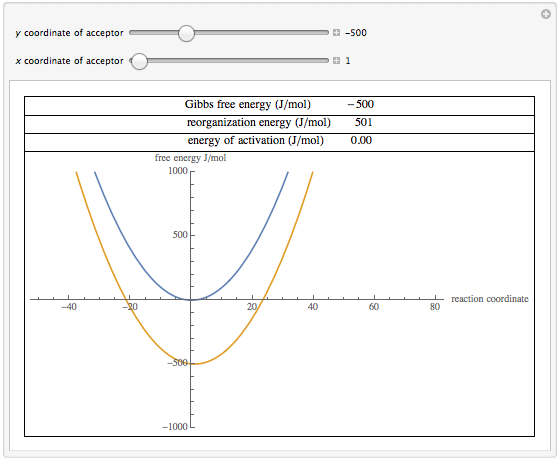
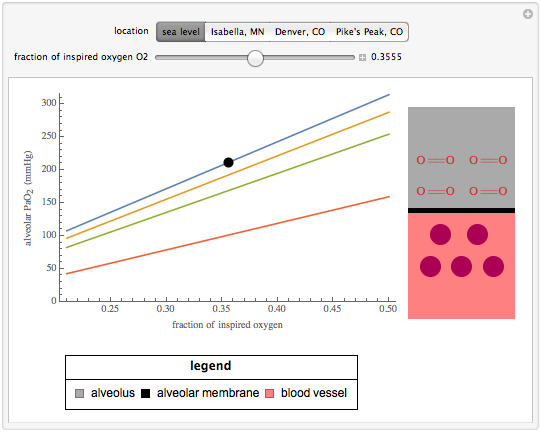
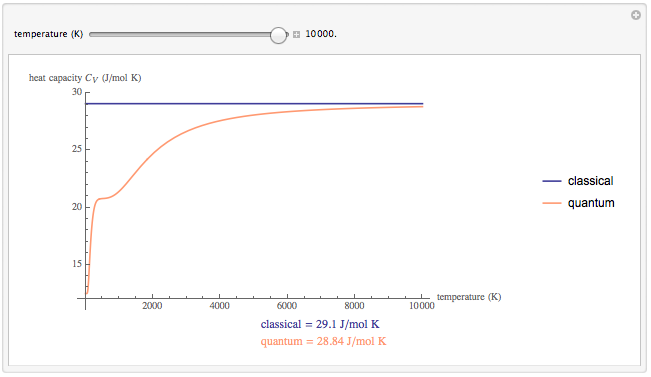
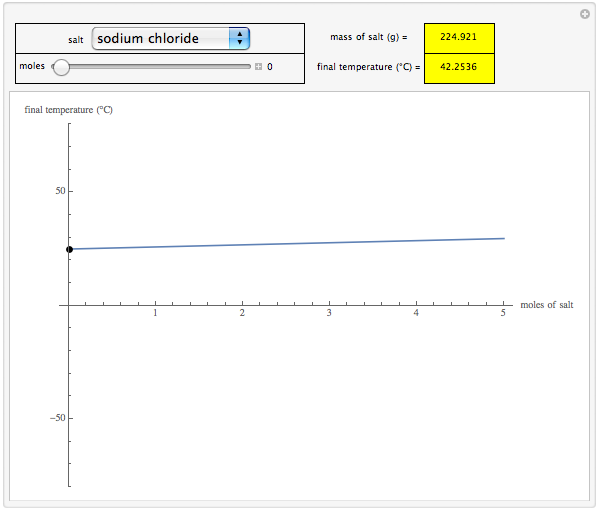
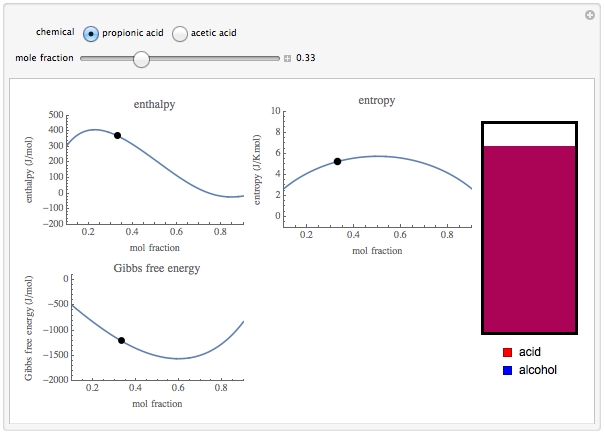
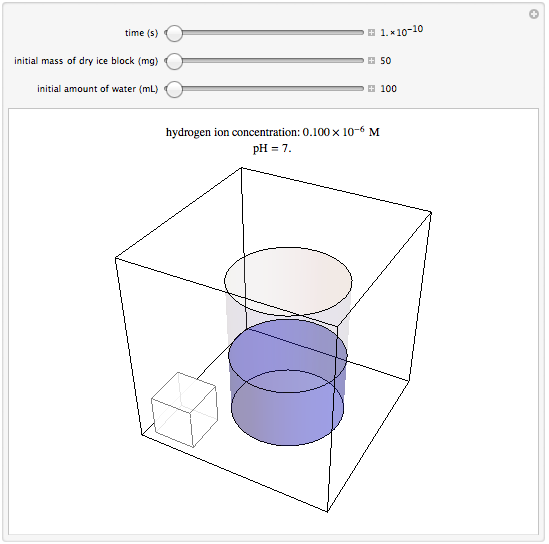
Wolfram Demonstrations Project

 Isobaric Compression and Expansion of an Ideal Gas

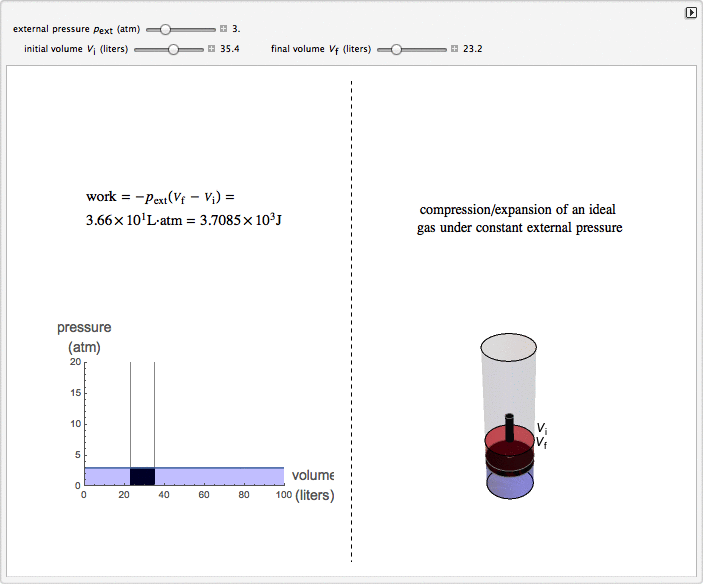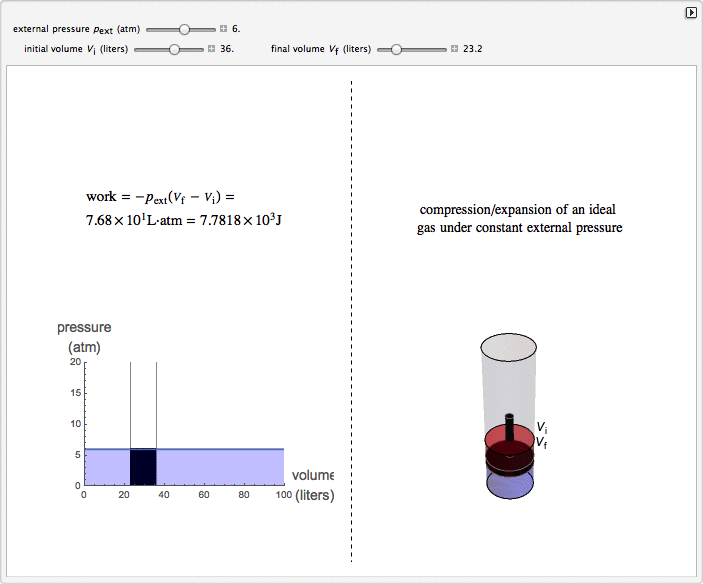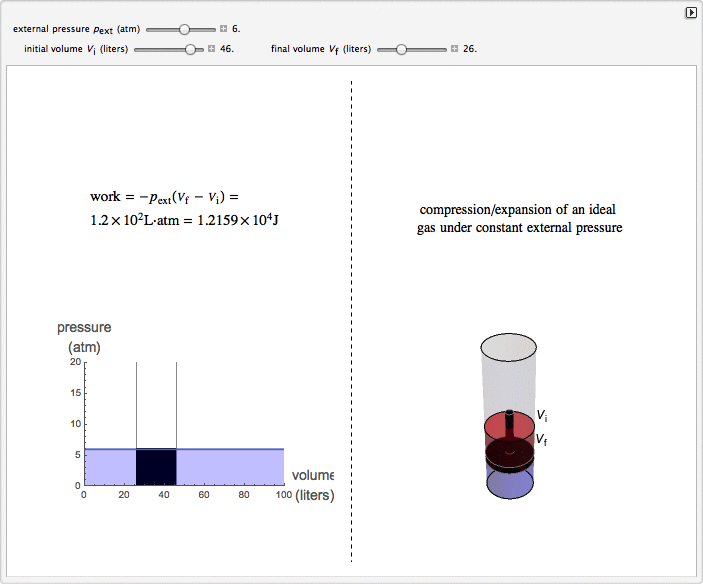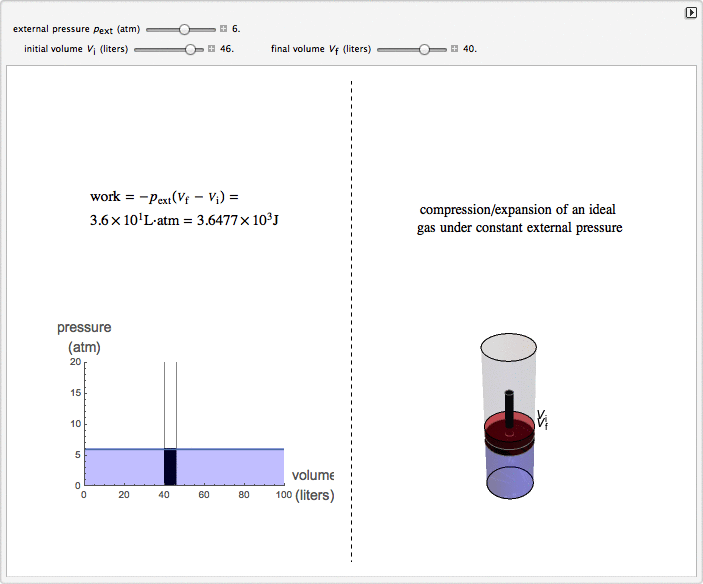
This Demonstration considers the isobaric thermodynamic process of compressing or expanding an ideal gas. Assume that a constant external pressure acts on the piston containing the gas. As you vary the external pressure, the horizontal line in the graph changes accordingly. When the variables for the initial and final volumes are changed, the position of the gridlines on the graph and the initial and final position of the head of the piston move. Work is calculated in the Demonstration with the convention used in chemistry: when the ideal gas expands, the work done is negative (i.e. the ideal gas "loses" energy), and vice versa.

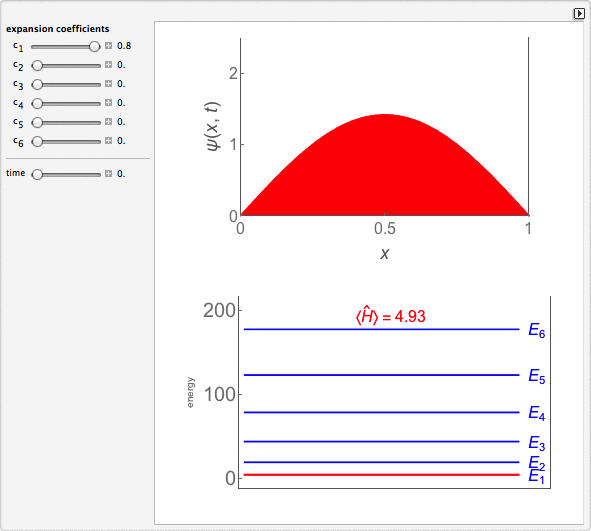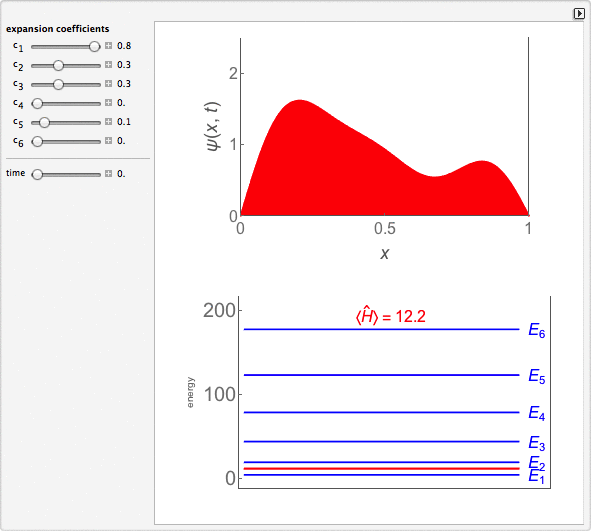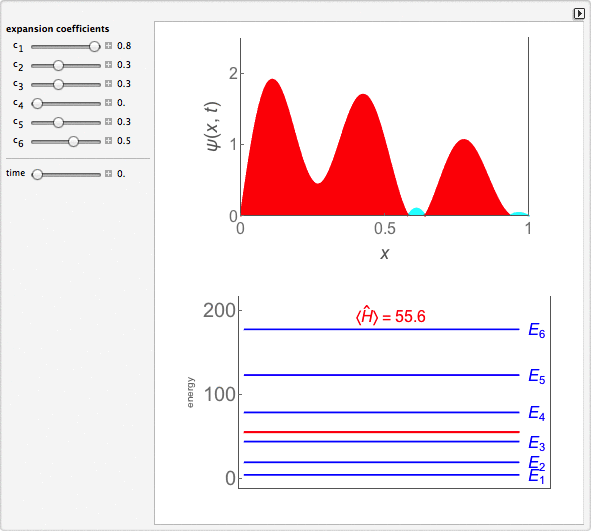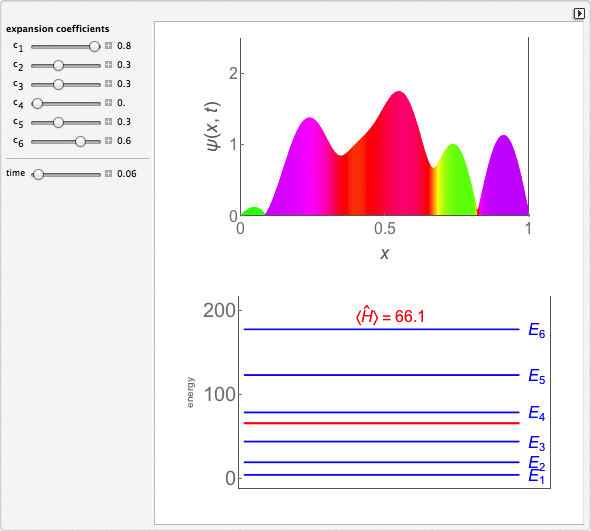
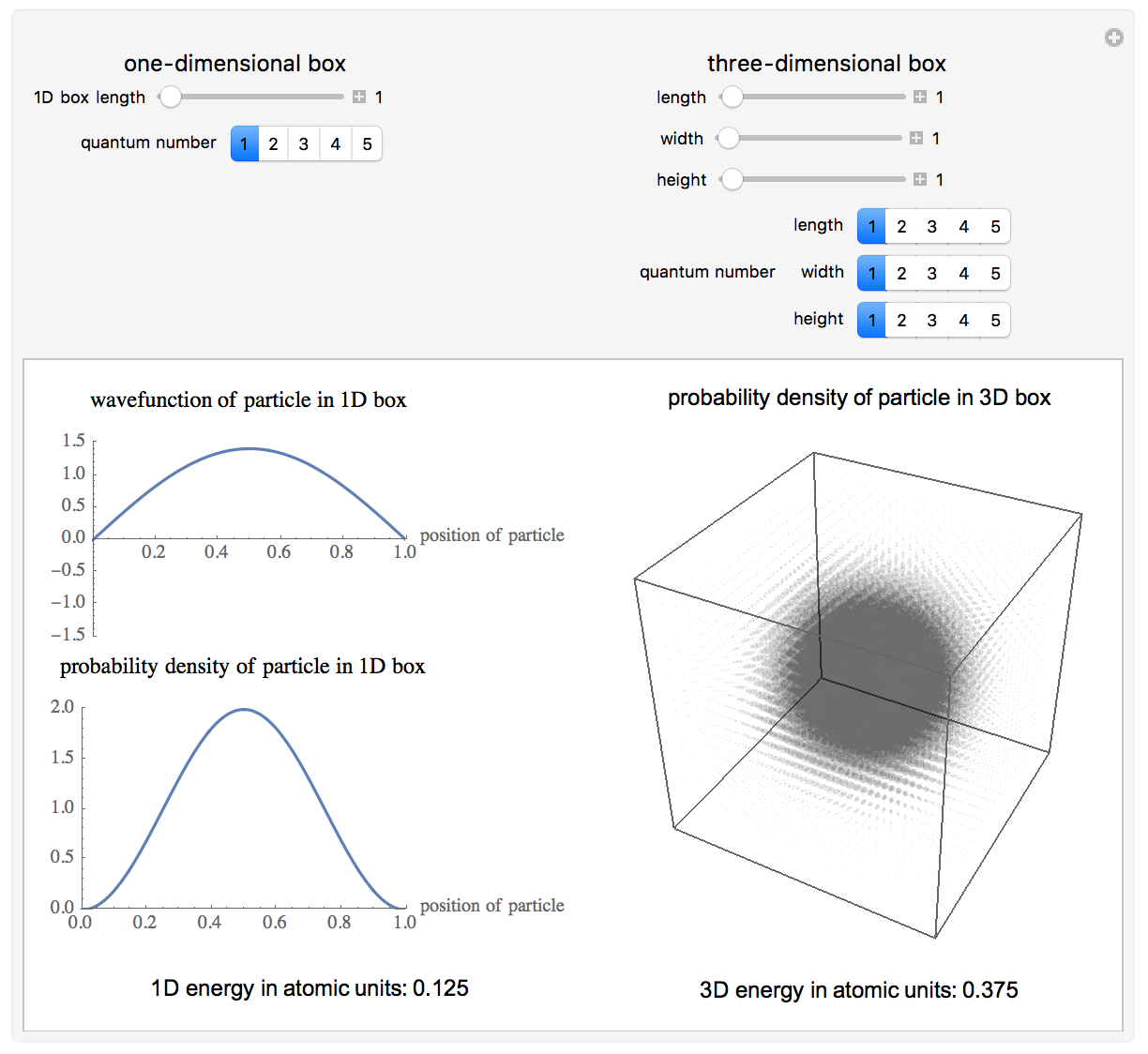
Time-Dependent Superposition of PIAB Eigenstates

This Demonstration looks at a time-dependent superposition of quantum particle-in-a-box eigenstates. The upper panel shows the complex wavefunction, where the shape is its modulus and the coloring is according to its argument (the range 0 to 2π corresponds to colors from red to magenta). The lower panel shows the eigenenergies in blue and the energy of the superposition state in red.

Compute-to-Learn Demonstrations

Particles in 1D and 3D Boxes

This Demonstration treats the quantum-mechanical problems of a particle in a box. We consider both the one-dimensional and three-dimensional cases.

Qualitative and Quantitative Aspects of Phase Transitions in Water

This Demonstration shows both the qualitative and quantitative behavior of phase changes in water

 

Nucleation Rates For CdSe Nanoparticles

This Demonstration shows how these nucleation conditions can be altered by varying the parameters of temperature and composition in crystalline media.

Alpha-Type Stirling Engine

A Stirling engine takes advantage of the thermodynamic properties of compression and expansion of gases to produce work. This Demonstration tracks the changes in pressure (atm) and volume (L) of the working fluid during a reversible Stirling cycle

 

Hair and Relative Humidity

This demonstration shows relative humidity and how it affects our daily lives, particularly what it does to our hair.

Effect of Temperature on Partial Miscibility in a Binary-Liquid System

Effect of Temperature on Partial Miscibility in a Binary-Liquid System This Demonstration shows how the mole fraction of a binary liquid system, composed of two partially miscible liquids, changes with temperature.

 

Marcus Theory Of Electron Transfer Reactions

This Demonstration shows the theory proposed by R. A. Marcus in 1956 [1–3] which provides a method to calculate the activation energy of a reaction by using a parabolic model to calculate activation energy.

Effect of Altitude on Alveolar Oxygen Pressure

This Demonstration shows the effects of changes in altitude on alveolar oxygen pressure using the alveolar gas equation.

 

Temperature Variation of Heat Capacity for an Ideal Diatomic Gas

This Demonstration considers the variation of heat capacity of an ideal diatomic gas, specifically hydrogen, with temperature.

Salt Packs for Heating or Cooling

This Demonstration shows the heating or cooling effects achieved by salt packs.

 

Liquid-Liquid Miscibility for Organic Acids with Methanol

This Demonstration shows Liquid miscibility, which is the measure of how well a pair of liquids mixes/dissolves

Carbon Dioxide Sublimation and Dissolution in Water

This Demonstration shows carbon dioxide sublimation from dry ice is a well-known phenomenon, which occurs at standard temperature and pressure.

 

Evaporation of Water from a Wet T-Shirt

This Demonstration shows how the rate of evaporation of water from a flat surface changes with temperature, wind speed, drying time, solar irradiance, air pressure and relative humidity.

Dissolution of Common Medications as Modeled by Drug Release Kinetics

This Demonstration considers the rate of dissolution of three drugs in everyday use, modeled by a tablet dissolving in a beaker of water.

 

Maximum Heat Transfer by Liquids at Different Temperatures

This Demonstration manipulates the initial temperature and mass of a sample of liquid to calculate the maximum quantity of heat it can transfer when its temperature changes.

Color Tuning of CdSe Semiconductor Nanocrystals

This Demonstration shows the effect of radius on the band gap energy of CdSe in quantum dots that emit in the visible light range under excitation with UV.

 

 

 

Diffusion of Gases in a Tube

This Demonstration shows the diffusion of two gases from opposite ends of a tube.

Rate of Cellular Respiration as a Function of Temperature and Cell Type

This Demonstration examines the rates of respiration as a function of cell type and temperature, displaying an animation of the cell with oxygen input and water output from mitochondria.

 

 

Henry's Law for Oxygen and Carbon Dioxide

This Demonstration considers the solubility of two different gases, CO2 and O2, in water.

Fick's Law Applied to Pulmonary Fibrosis

This Demonstration shows the rate of diffusion in an alveolus using Fick's law.

 

 

Carbon Dioxide Sublimation and Dissolution Equilibria

This Demonstration manipulates the number of moles of CO2 and the temperature to visualize the equilibria of sublimation of solid CO2 and the dissolution of gaseous CO2 into aqueous solution.

Diffusion of Oxygen Molecules across a Membrane Using Fick's Law

This Demonstration shows the diffusion of oxygen molecules across a membrane (represented by a box) according to Fick’s law.

 

 

Simulating Gas Exchange in a Model of Pulmonary Fibrosis

This Demonstration displays the rate at which the gas molecules of carbon dioxide and oxygen diffuse through the alveolar wall as a function of alveolar thickness.

Electron in a Nanocrystal Modeled by a Quantum Particle in a Sphere

This Demonstration shows the quantum effects observed on a single electron trapped in a spherical nanoparticle, modeled as a particle in a sphere.

 

 

Heat Flow Between a Human and a Chair

This Demonstration shows the equilibration between two objects (a human and a chair) at different temperatures in thermal contact with one another.

Heat Flow Between Two Reservoirs

This Demonstration illustrates the heat transfer between two vessels containing water, in thermal contact with one another.

 

 

Other Demonstrations

Compute-to-Learn University of Michigan Ann Arbor, MI 48109

(734) 763-8012
eitan@umich.edu

© 2015 Compute-to-Learn | Design by W3layouts