| Conversion | top |
Consider the general equation
The basis of calculation is always the limiting reactant. We will choose A as our basis of calculation and divide through by the stoichiometric coefficient to put everything on the basis of "per mole of A".
The
conversion X of species A in a reaction is equal to the number of moles
of A reacted per mole of A fed, ie
| Batch | Flow | |
|---|---|---|
|
|
|
What is the maximum value of conversion?
For irreversible reactions, the maximum value of conversion, X, is that for
complete conversion, i.e. X=1.0.
For reversible reactions, the maximum value of conversion, X, is the equilibrium
conversion, i.e. X=Xe.
Batch: Moles A remaining = NA = Moles A initially - Moles A reacted
NA= NA0 - moles A initially x (moles A reacted)/(moles A fed)
| NA = NA0 - NA0X |
Flow: Rate of Moles of A leaving FA = Rate of Moles of A fed - Rate of Moles of A reacted =
| FA = FA0 - FA0X |
| Design Equations (p. 34-41) | top |
The design equations presented in Chapter 1 can also be written in terms of conversion. The following design equations are for single reactions only. Design equations for multiple reactions will be discussed later.
| Reactor | Differential | Algebraic | Integral | ||
|---|---|---|---|---|---|
| Batch |
|
|
|

|
|
| CSTR |
|
|
|||
| PFR |
|
|
|
||
| PBR |
|
|
|
|
| Reactor Sizing (p. 41-56) | top |
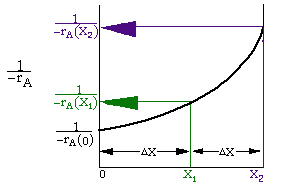
By sizing a chemical reactor we mean we're either detering the reactor volume to achieve a given conversion or determine the conversion that can be achieved in a given reactor type and size. Here we will assume that we will be given -rA= f(X) and FA0. In chapter 3 we show how to find -rA= f(X).
Given -rA as a function of conversion,-rA=f(X),
one can size any type of reactor. We do this by constructing a
Levenspiel plot. Here we plot either![]() or
or![]() as a function of
X. For
as a function of
X. For![]() vs. X, the volume of a CSTR and
the volume of a PFR can be represented as the shaded areas in the
Levenspiel Plots shown below:
vs. X, the volume of a CSTR and
the volume of a PFR can be represented as the shaded areas in the
Levenspiel Plots shown below:
| Numerical Evaluation of Integrals (Appendix A.4) | top |
The integral to calculate the PFR volume can be evaluated using a method such as Simpson's One-Third Rule (pg 1014):
 |
NOTE: The intervals
( |
Simpson's One-Third Rule is one of the more common numerical methods. It uses three data points. Other numerical methods (see Appendix A, pp 1009-1015) for evaluating integrals are:
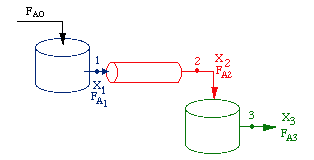
| Reactors in Series | top |
Given -rA as a function of conversion, one can also design any sequence of reactors:
|
Only valid if there are no side streams |
Consider a PFR between two CSTRs
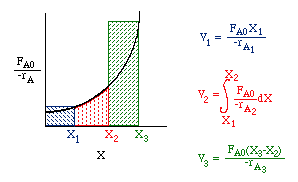
| Space Time (p. 57) | top |
The Space time, tau, is obtained by dividing the reactor volume by the volumetric flow rate entering the reactor:
![]()
Space time is the time necessary to process one volume of reactor fluid at the entrance conditions. This is the time it takes for the amount of fluid that takes up the entire volume of the reactor to either completely enter or completely exit the reactor.
| Reaction |
Reactor | Temperature | Pressure atm | Space Time | |
| (1) | C2H6 → C2H4 + H2 |
PFR | 860°C | 2 | 1 s |
| (2) | CH3CH2OH + HCH3COOH → CH3CH2COOCH3 + H2O |
CSTR | 100°C | 1 | 2 h |
| (3) | Catalytic cracking | PBR | 490°C | 20 | 1 s < τ < 400 s |
| (4) | C6H5CH2CH3 → C6H5CH = CH2 + H2 | PBR | 600°C | 1 | 0.2 s |
| (5) | CO + H2O → CO2 + H2 | PBR | 300°C | 26 | 4.5 s |
| (6) | C6H6 + HNO3 → C6H5NO2 + H2O | CSTR | 50°C | 1 | 20 min |
| Useful Links | top |
* All chapter references are for the 4th Edition of the text Elements of Chemical Reaction Engineering.