Solutions
How many pound moles of gas are in the system we have chosen for the Los Angeles basin if the temperature is 75°F and the pressure is 1 atm?
DATA
°
What is the rate, , at which all autos emit carbon monoxide into the basin ()?
DATA
Cars =
P = 1 atm
V @ std
T @ std º
Molar % CO =
What is the volumetric flow rate of a 15 mph wind through the corridor 20 miles wide and 2000 feet high?
DATA
Assuming that the volumetric flow rates entering and leaving the basin are identical show that the unsteady mole balance on CO within the basin becomes:
From the general material balance equation:
Therefore, substitution yields:Input – Output + Generation – Consumption = AccumulationInput
Output
Generation = 0
Consumption = 0
Accumulation =
Verify that the solution to the previous equation is
Starting from the equation obtained in part e, we must first separate variables by solving for , which is the value that we are trying to obtain. We might as well assume that and are a constant factor.
, the total volume of air in the Basin, is considered to be constant. and represent a specific volumetric flow rate multiplied by a specific concentration (), which is also constant:
Only and remain as the last variables in the equation. Let = to simplify mathematical procedures. Let to represent a constant term. Let .
We can know integrate the equation.
If the initial concentration of carbon monoxide in the Los Angeles basin before the Santa Ana wind starts to blow is 8 ppm , calculate the time required for the carbon monoxide to reach a level of 2 ppm.
DATA
There is heavier traffic in the L.A. basin in the mornings and in the evenings as workers go to and from work in downtown L.A. Consequently, the flow of CO into the L.A. basin might be better represented by the sine function over a 24-hour period.
The time, t = 0, starts at midnight. Where a = 35,000 and b = 30,000 . The general material balance equation now becomes
(Sine function, original conditions)
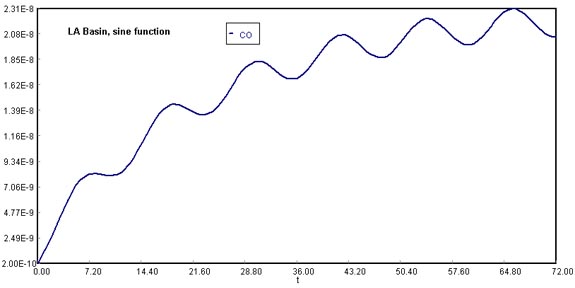
Download the original Polymath file of this problem, by clicking here: LA Basin, sine function Use Polymath
Smog begins to build up again immediately after a Santa Ana wind passes through the basin. The volumetric flow rate through the basin has dropped to (1.5 mph). Plot the concentration of carbon monoxide in the basin as a function of time for up to 72 hours and just after a Santa Ana wind. The initial concentration of CO is 0.08 ppm .
(Assuming wind stops blowing after 72 h)
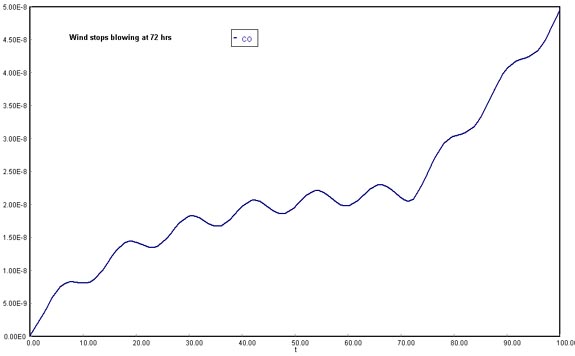
Download the original Polymath file of this problem, by clicking here: LA Basin, 72 h Considering that the Santa Ana wind provides a means of cleansing and lowering CO concentration in the Los Angeles Basin, once the current stops being available there would be no vehicle to dilute the air contaminants. Therefore, CO molecules would start to accumulate in the fixed volume of the system. This shows in the steep rise of carbon monoxide concentrations after 72 h.
Plot the concentration of carbon monoxide as a function of time up to 48 hours for the case when a Santa Ana wind begins to blow after the 48 hours buildup of CO.
(Assuming wind is not blowing until 48 h, and then resumes at )
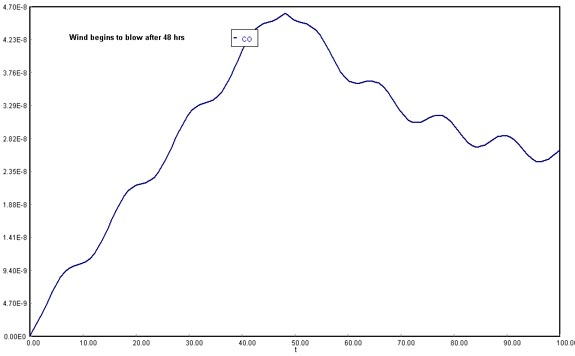
Download the original Polymath file of this problem, by clicking here: LA Basin, 48 hrs The opposite phenomenon occurs once the wind starts blowing: with the possibility of venting out the accumulated gases in the Los Angeles Basin, the CO concentration will decrease abruptly. However, in the long run, it will increase again and stabilize.
Vary the parameters, , and write a paragraph describing what you find.

Download the original Polymath file of this problem, by clicking here: LA Basin, vo variations Using at 1.67E+11 , 1.67E+12 , and 1.67E+13 , we found an inversely proportional relationship between CO accumulation and volumetric flow rate of the Santa Ana wind. Thus, when vo is the lowest, CO accumulation presents a steeper slope than the other runs. It is important to note that at vo = 1.67E+13 , a stabilizing condition occurs, meaning that the amount of CO released by vehicles becomes negligible.
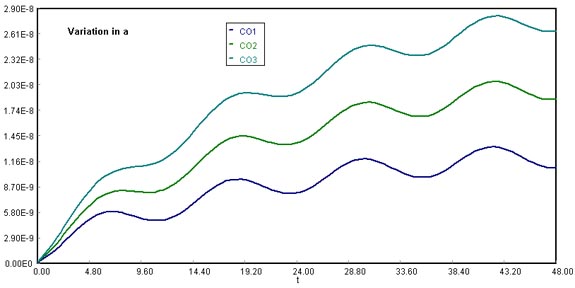
Download the original Polymath file of this problem, by clicking here: LA Basin, a variations Using at 20000 , 35000 , and 50000 , we notice that the final CO accumulation varies proportionally with the magnitude chosen. This happens because as the sine function for CO emissions in cars spreads over time, the accumulation tends to equal the y-axis intercept (a) of the sine function.
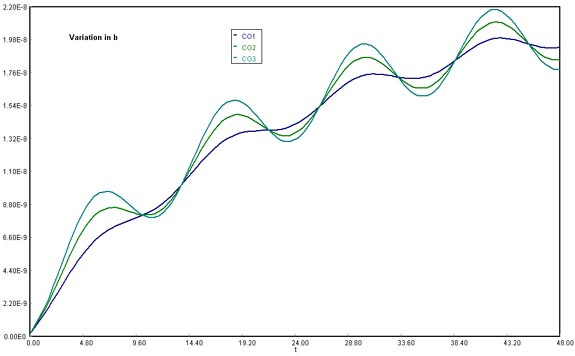
Download the original Polymath file of this problem, by clicking here: LA Basin, b variations Using b at 15000 lbmol CO/h, 35000 lbmol CO/h, and 50000 lbmol CO/h, the amplitude of the variation in CO accumulation increased directly as the values for b became higher. This would be explained mathematically by remembering that the b multiplies the sine function directly, meaning that it accounts for its degree of amplitude from reference to lowest/highest crest.
Alejandra De Obeso, Lauren Floyd, Dr. Nihat M. Gürmen, Prof. H. Scott Fogler