© Timothy E. Chupp, 1995
We now have a feel for energy and for conversion of one form of energy to another
(for example from chemical energy to heat). Work is the energy transferred from
an agent applying a force to an object or into heat, and the net work done
on an object is the
total change of kinetic energy. Both positive work and negative work have
meaning:
Positive work follows when the force has a component parallel to the displacement. Positive
work adds energy to a system.
Negative work follows when the force has a component opposite or against the displacement.
Negative work removes or dissipates energy from the system.
Two examples: In pulling a box of books along a rough floor at constant velocity, I do positive work on the box, that is I put energy into the system. The force of friction opposes the displacement (always), and does negative work. The net work is the total of my positive work and fiction's negative work, i.e. ZERO. Thus the Kinetic energy of the box does not change: its velocity remains constant.
Another experience: When pushing a car to speed it up for a jump start, we push on the car in the direction it is moving, that is we do positive work. It is also possible to slow a car down by pushing on it. In this case we push opposite the direction of motion. We do negative work, which removes kinetic energy from the system.
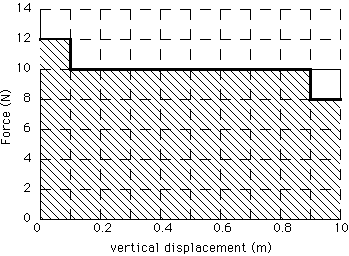
Consider the simple task of lifting a book from the floor to a convenient height, say to a 1 meter high counter top. The process involves first accelerating the book upward from rest 0.1 m, then moving it with a constant upward velocity for 0.8 m, and finally accelerating the book downward (that is decelerating it) to bring it to rest 1 m above the floor. It is convenient to show this task on a graph of the applied force versus displacement. This is now a very meaningful graph on which the area "under" the curve is a measure of the work.

Figure 1: A graph of applied force vs displacement for the task of lifting a 1 kg book a total of 1 m above the floor.
Let's discuss several aspects of this graph: Over the first 0.1 m, the book
is accelerating upward, which requires an imbalance of the upward applied
force (12 N) and the downward force of gravity (-10 N). The work done
by the applied force is 12 N x 0.1 m = 1.2 J. The net
work done is (12 N - 10 N) x 0.1 m = 0.2 J. This net work
is the change in KE of the book. (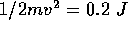 so
so 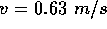 ). The
work done over the 0.8 m from 0.1 m to 0.9 m is 10 N x 0.8 m = 8 J,
but the net force is ZERO so the net work is ZERO. Over the final 0.1 m, the
applied force of 8 N does 0.8 J of work, but the net work is
(8 N - 10 N) x 0.1 m = -0.2 J, that is the change in KE is
negative 0.2 J bringing the KE and velocity to ZERO. The
total area under the applied force vs velocity curve is 0.2 + 8 + 0.8 = 10 J, and
the net work, that is the net change in KE, is ZERO.
This would be the case for any combination of acceleration and deceleration.
Try it.
). The
work done over the 0.8 m from 0.1 m to 0.9 m is 10 N x 0.8 m = 8 J,
but the net force is ZERO so the net work is ZERO. Over the final 0.1 m, the
applied force of 8 N does 0.8 J of work, but the net work is
(8 N - 10 N) x 0.1 m = -0.2 J, that is the change in KE is
negative 0.2 J bringing the KE and velocity to ZERO. The
total area under the applied force vs velocity curve is 0.2 + 8 + 0.8 = 10 J, and
the net work, that is the net change in KE, is ZERO.
This would be the case for any combination of acceleration and deceleration.
Try it.
Now that the book is at the height of 1 m above the floor, having had some work done to get it there, the energy used can be converted to kinetic energy by dropping the book. When the book is dropped, its velocity and KE increase as it falls until it hits the floor with a bang or a splat. In the process of hitting the floor the Kinetic Energy is converted into other kinds of energy such as heat, sound and perhaps some work that permanently deforms the shape of the book. Before the book is dropped, the work done in lifting it is stored. This stored energy is available for conversion into KE, heat energy, sound energy, etc. We often call this stored energy Potential Energy or position dependent energy: PE. It is also properly called gravitational potential energy (to distinguish it from electrical potential energy) and, as we'll define it soon (Lecture 16), in terms of the change of gravitational binding energy.
The stored PE is given by the total work done in lifting the book, that is by the total area under the curve of applied force vs position. To be exact, we say
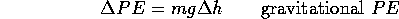
Only the change of energy, and the change of PE, make sense. However, we often define a certain position as our reference point, i.e. h=0 with PE=0 at h=0. Adopting this convention,

For example, the floor is at h=0.
The work done in lifting a book can be stored as PE and then recovered. This is true no matter how the book was lifted, that is if it was accelerated and decelerated rapidly or slowly. In principle, we could lift and horizontally translate the book so that it is stored at a height h, but with a horizontal displacement. Since the book must first gain and then lose some horizontal velocity, first positive and then negative work is done on the book by who or what moves it. In many practical cases, the positive work is not actually "recovered," that is it is not stored in the same way that gravitational PE is stored. This is why it is often emphasized that "the book is moved horizontally very slowly," so that the extra work done is so small as to be negligible.
In cases for which the work done by an applied force can be completely stored as PE, we say that work is done against a conservative force. In the case of the book, the conservative force is gravity. Electrical forces are conservative, but frictional forces are not.
We will consider a large number of examples, including that of lifting the book, that
demonstrate the Conservation Law of Mass/Energy. This law is best stated that
any system has a total energy E that remains constant. The total energy is the
sum of KE, stored energy (PE), heat, sound, 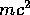 etc. In fact heat and sound and
many other forms of energy are manifestations of motion, that is of the molecules
of an object and of air. The contribution
etc. In fact heat and sound and
many other forms of energy are manifestations of motion, that is of the molecules
of an object and of air. The contribution 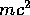 to E will be discussed more
in Lecture 16. Conservation of energy can be expressed as follows:
to E will be discussed more
in Lecture 16. Conservation of energy can be expressed as follows:
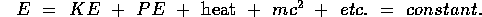
A long massive pendulum is a good example of conservation of energy because the amount of heat energy generated each cycle can be quite small compared to the maximum KE and PE. Focault used a pendulum, with a special pivot, that always swings in the same plane so that one can observe the earth turning underneath the pendulum swing during many hours, even days. As you observe the pendulum swing, you can watch energy converted from PE to KE to PE etc. as shown. If you watch long enough or there is appreciable friction, you will discern that energyy is also converted into heat.
Neglecting this production of heat, that is neglecting friction, we can write the total energy and conservation of energy as
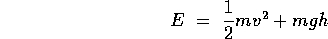
Where h is measured above the lowest point. Note that the maximum KE occurs at h=0 and the maximum PE occurs where v=0, that is
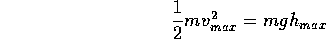
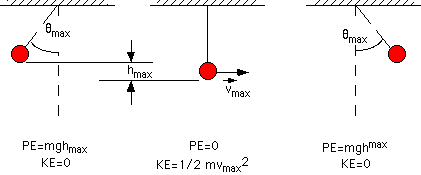
Figure 2: The pendulum Bob at three positions. The KE and PE are indicated at each position.
Let's explore this example a bit further. To do so, we consider the free body diagram for the pendulum Bob including the tension in the pendulum wire and the gravitational force on Bob. This leads to:

At the lowest point of the swing, when the velocity has its maximum magnitude, the acceleration is centripetal, and directed straight up with magnitude

Substituting and noticing that 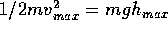 ,
,
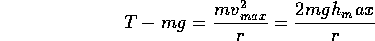
We can solve for the tension
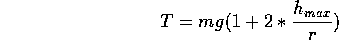
Thus T the tension in the pendulum wire depends on the velocity, and is maximum when the KE is greatest, that is at the lowest point of the pendulums swing.
An interesting demonstration of this, and thus a way to confirm our application of conservation of energy to the pendulum Bob, is the set-up with a 1 kg Bob and a second, 2 kg mass (Pat) connected to the pendulum wire by way of a pulley as shown.
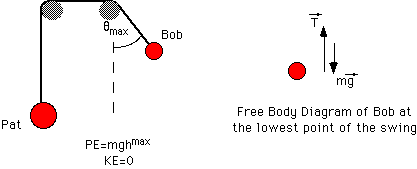
 the swinging Bob can raise
Pat.
the swinging Bob can raise
Pat.
Pat will inform us when the tension in the string is greater than 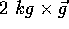 (the product of Pat's mass and the local gravitational field). This happens when
(the product of Pat's mass and the local gravitational field). This happens when
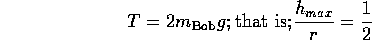
With the help of a little trigonometry, you can see that
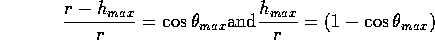
And
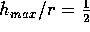 when
when 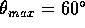 .
.
When we tried this in lecture, we found that 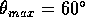 was not quite enough, because it is not true that "no energy is lost due to friction," even for
a half-swing of the pendulum. When we made the angle
was not quite enough, because it is not true that "no energy is lost due to friction," even for
a half-swing of the pendulum. When we made the angle 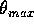 slightly
greater than
slightly
greater than 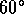 , Pat was lifted a bit.
, Pat was lifted a bit.
Return to Physics 125